Advanced Algo Trading: Machine Learning for Quant Traders

Deep Learning & Random Forest Strategies for S&P 500 Forecasting

Dec 10, 2025

∙ Paid

Welcome to this algorithmic trading project! This repository implements advanced quantitative strategies using Long Short-Term Memory (LSTM) networks and Random Forests (RF) to forecast the directional movements of S&P 500 stocks.

Download link at the end of article. Use the button to download all of python file and datasets.

The core objective is to predict whether a stock will be a top performer (top 50%) or a bottom performer (bottom 50%) for a given trading session. Based on these predictions, the system simulates a Long-Short Equity Strategy:

Long (Buy): Top 10 predicted stocks.
Short (Sell): Bottom 10 predicted stocks.

📂 Project Layout

The project is organized into modular scripts for different models and trading horizons, supported by a central statistical analysis toolkit.

data/: Contains the input data (Open and Close prices for S&P 500 constituents).
results-*/: (Generated) Stores simulation results, including daily returns and performance metrics.
models-*/: (Generated) Stores trained model checkpoints and logs.

📖 File Guide & Reading Order

To understand this project, we recommend reading the files in the following order. Each script is self-contained but builds upon shared concepts.

The Core Toolkit

Statistics.py
What it is: The backbone of the project’s performance analysis.
What it does: It takes the daily returns generated by any trading strategy and calculates key financial metrics like Sharpe Ratio, Value at Risk (VaR), Maximum Drawdown (MDD), and Alpha. You will see this class imported and used at the end of every trading script to evaluate success.

Intraday Trading Models (Open-to-Close)

These models predict price movements within a single trading day (from Market Open to Market Close).

train_intraday_lstm.py (Recommended First Read)
Model: Single-feature LSTM.
Features: Uses the past 240 days of intraday returns as input.
Goal: Predict if a stock will outperform intraday.
Key Concept: This is the baseline Deep Learning model. Read this to understand the data pipeline: create_label (labeling stocks winner/loser), create_stock_data (creating lag features), and simulate (the trading loop).
train_intraday_lstm_multi.py
Model: Multi-feature LSTM (The “Advanced” Model).
Features: Uses 3 distinct feature sets for the past 240 days:

Intraday Returns (Open to Close)
Overnight Returns (Previous Close to Open)
Daily Returns (Close to Close)

Why read it: It shows how to engineer a rich feature set to capture different market dynamics (momentum, gaps, trends).
train_intraday_rf.py
Model: Random Forest Classifier.
Difference: Instead of a sequence model like LSTM, this uses a tree-based ensemble. It treats the 240 days as 240 separate input features. It’s a faster, non-deep-learning benchmark.
train_intraday_rf_multi.py
Model: Random Forest with the 3-feature set.
Goal: Combines the robust feature engineering of the 3-stream approach with the stability of Random Forests.

Next-Day Trading Models (Close-to-Close)

These models forecast the return from today’s close to tomorrow’s close.

train_nextday_lstm.py
Model: Single-feature LSTM.
Features: Uses past daily (close-to-close) returns.
Key Difference: The target variable uses pct_change() on Closing prices, meaning it holds positions overnight, exposing the strategy to gap risk but capturing multi-day trends.
train_nextday_rf.py
Model: Random Forest for next-day prediction.
Goal: The tree-based benchmark for the overnight holding strategy.

🚀 How to Run

First Download the entire source code all of the files from here:

Use the button at the end of this article to download source code and run it:

Install Requirements (Legacy Environment Recommended)

pip install scikit-learn==0.20.4 pip install tensorflow==1.14.0 pip install pandas numpy scipy

Execute a Strategy: To train the baseline Intraday LSTM model and backtest it from 1993 to 2019:

python train_intraday_lstm.py

Check Results: After execution, check the newly created results-Intraday-240-1-LSTM/ folder for:

avg_returns.txt: Yearly performance summaries (Mean Return, Sharpe Ratio).
avg_daily_rets-*.csv: Detailed daily P&L for further analysis.

Let’s start with Statistics.py

def __init__(self,series):
       
        self.series = np.array(series)
        self.n = len(series)

The constructor method initializes a Statistics object by accepting a series of returns as input and storing it for subsequent analysis. This method is called automatically when creating a new Statistics instance in the trading scripts, typically with the combined daily returns from both long and short positions. The method first converts the input series into a numpy array to ensure consistent numerical operations regardless of whether the input is a pandas Series, list, or other iterable type. It then stores the length of the series in the instance variable n, which is used by various other methods to calculate percentages and indices. For example, when a trading script calls Statistics(returns.sum(axis=1)), this constructor receives the summed daily returns, converts them to a numpy array, and counts how many trading days are in the series, making this information readily available for all subsequent statistical calculations without needing to recompute it.

def mean(self):
        return np.mean(self.series)

The mean method calculates and returns the arithmetic average of all returns in the series, representing the expected daily return of the trading strategy. This is one of the most fundamental performance metrics used in finance, as it tells us on average how much profit or loss the strategy generates per trading day. The method uses numpy’s mean function which sums all the values in the series and divides by the count, giving us the central tendency of the return distribution. This metric is used extensively in the trading scripts’ output files where it’s saved to the avg_returns.txt file for each test year, and it’s also a key component in calculating the Sharpe ratio. For instance, if the mean returns 0.0005, it means the strategy earns an average of 0.05 percent per day, which when annualized over approximately 252 trading days would represent a significant annual return. The mean is called by the shortreport and report methods to display performance summaries, and it’s also used internally by the sharpe method to compute risk-adjusted returns.

def std(self):
        return np.std(self.series)

The std method computes the standard deviation of the return series, which measures the volatility or risk of the trading strategy by quantifying how much the daily returns deviate from their mean value. Standard deviation is a critical risk metric in finance because it captures the uncertainty and variability in returns, with higher values indicating more volatile and potentially riskier strategies. The method uses numpy’s std function which calculates the square root of the variance, where variance is the average of the squared differences from the mean. This metric appears in both the shortreport and report output methods and is also used as the denominator in the Sharpe ratio calculation, making it essential for risk-adjusted performance evaluation. For example, if the standard deviation is 0.02, it means that on a typical day, the strategy’s return deviates from its average by about 2 percent in either direction. A strategy with high mean returns but also high standard deviation might be less desirable than one with moderate returns and low volatility, which is why this metric is always considered alongside the mean when evaluating trading performance.

    def stderr(self):
        return scipy.stats.sem(self.series)

The stderr method calculates the standard error of the mean, which quantifies the precision of the sample mean as an estimate of the true population mean of returns. Unlike standard deviation which measures the variability of individual returns, standard error measures how much the calculated mean might vary if we were to repeat the trading experiment with different time periods. The method uses scipy’s sem function which computes the standard error by dividing the standard deviation by the square root of the sample size, following the formula stderr equals sigma divided by square root of n. This metric is particularly useful for statistical inference and hypothesis testing, as it helps determine whether the observed mean return is significantly different from zero or from other benchmarks. The standard error appears in the comprehensive report method output and becomes smaller as the number of observations increases, reflecting greater confidence in the estimated mean. For instance, with 252 trading days in a year, the standard error would be the daily standard deviation divided by the square root of 252, which is approximately 15.87, giving us a measure of how reliable our annual performance estimate is based on daily observations.

    def percentiles(self,p=[.25,.5,.75]):
        return pd.Series(self.series).describe(percentiles=p)

The percentiles method generates a comprehensive statistical summary of the return distribution including count, mean, standard deviation, minimum, maximum, and specified percentile values, providing a complete picture of how returns are distributed across their range. By default, it calculates the 25th percentile (first quartile), 50th percentile (median), and 75th percentile (third quartile), which divide the sorted returns into four equal parts and help identify the spread and symmetry of the distribution. The method converts the numpy array to a pandas Series and calls the describe function with custom percentiles, which internally sorts the data and finds the values at the specified positions. This is particularly useful for understanding the full distribution of returns beyond just mean and standard deviation, as it reveals whether returns are symmetric or skewed, and whether there are extreme outliers. The output appears in the comprehensive report method and helps traders understand questions like what return can be expected on a typical good day versus a typical bad day, or what percentage of days fall within certain return ranges. For example, if the 25th percentile is negative 1 percent and the 75th percentile is positive 1.5 percent, it tells us that the middle 50 percent of trading days had returns between these values, with 25 percent of days performing worse and 25 percent performing better.

    def pos_perc(self):
        return 100*sum(self.series>0)/self.n

The pos_perc method calculates the percentage of trading days that generated positive returns, which is an important measure of the strategy’s consistency and win rate. This metric works by creating a boolean array where each element is True if the corresponding return is greater than zero and False otherwise, then summing these boolean values (where True counts as 1 and False as 0) to get the total number of profitable days, and finally dividing by the total number of days and multiplying by 100 to convert to a percentage. A strategy with a high positive percentage (above 50 percent) wins more often than it loses, though this doesn’t necessarily mean it’s more profitable overall since the magnitude of wins and losses also matters. This metric appears in the comprehensive report output and helps assess the psychological comfort of a trading strategy, as strategies with very low win rates can be difficult to follow even if they’re ultimately profitable due to occasional large wins. For example, if pos_perc returns 58.5, it means that on 58.5 percent of trading days the strategy made money, while on 41.5 percent of days it lost money, suggesting a moderately consistent strategy that wins slightly more often than it loses, which can be important for trader confidence and strategy adherence over long periods.

    def skewness(self):
        return scipy.stats.skew(self.series)

The skewness method measures the asymmetry of the return distribution, indicating whether returns are more likely to have extreme values on the positive or negative side. This metric uses scipy’s skew function which calculates the third standardized moment of the distribution, where a skewness of zero indicates a perfectly symmetric distribution like the normal distribution, positive skewness indicates a distribution with a long right tail (more extreme positive returns), and negative skewness indicates a long left tail (more extreme negative returns). In trading, positive skewness is generally desirable because it means the strategy occasionally generates very large positive returns while losses tend to be more moderate, whereas negative skewness suggests the opposite pattern of occasional catastrophic losses. The skewness value appears in the comprehensive report output and helps traders understand the shape of their return distribution beyond just mean and variance. For example, a skewness of negative 0.5 would indicate a moderately left-skewed distribution where extreme losses are more common than extreme gains, which might be concerning for risk management, while a skewness of positive 1.2 would suggest a right-skewed distribution with occasional very profitable days, which is often preferred in trading strategies as it aligns with the goal of cutting losses short and letting winners run.

    def kurtosis(self):
        return scipy.stats.kurtosis(self.series)

The kurtosis method measures the tailedness of the return distribution, specifically quantifying how much probability mass is in the extreme tails compared to a normal distribution, which is crucial for understanding the likelihood of extreme events or outliers. This method uses scipy’s kurtosis function which calculates the fourth standardized moment and returns excess kurtosis (kurtosis minus 3), where a value of zero indicates tails similar to a normal distribution, positive values indicate heavier tails with more extreme outliers (leptokurtic), and negative values indicate lighter tails with fewer extremes (platykurtic). In financial markets, return distributions typically exhibit positive excess kurtosis, meaning extreme events (both gains and losses) occur more frequently than a normal distribution would predict, which has important implications for risk management and position sizing. The kurtosis value appears in the comprehensive report output and helps traders assess tail risk and the adequacy of risk models based on normal distribution assumptions. For instance, an excess kurtosis of 3.0 indicates significantly fatter tails than normal, suggesting that extreme daily returns (both very large gains and very large losses) happen much more often than would be expected under normality, which means risk metrics like standard deviation might underestimate the true risk of rare but severe losses, and traders should be prepared for occasional extreme movements beyond what typical volatility measures suggest.

    def VaR(self,confidence):
        indx = int(confidence*self.n/100)
        return sorted(self.series)[indx-1]

The VaR method calculates Value at Risk at a specified confidence level, which represents the maximum expected loss over a single trading day at that confidence level, making it one of the most widely used risk metrics in finance. The method works by first calculating the index position corresponding to the confidence level (for example, 5 percent confidence means we want the 5th percentile), then sorting all returns from worst to best, and finally returning the return value at that index position. This tells us that on the worst X percent of days, the loss was at least this bad, or conversely, that 100 minus X percent of days had returns better than this value. The method is called three times in the comprehensive report with confidence levels of 1, 2, and 5 percent to show increasingly severe tail risks. For example, if VaR(5) returns negative 0.03, it means that on the worst 5 percent of trading days, the strategy lost at least 3 percent, or equivalently, there’s a 5 percent chance on any given day of losing 3 percent or more. This metric is crucial for risk management and capital allocation decisions, as it provides a concrete number for potential losses that can be used to set position sizes, stop losses, and overall portfolio risk limits, though it’s important to note that VaR only tells us the threshold value and not how bad losses might be beyond that threshold.

    def CVaR(self,confidence):
        indx = int(confidence*self.n/100)
        return sum(sorted(self.series)[:indx])/indx

The CVaR method calculates Conditional Value at Risk, also known as Expected Shortfall, which measures the average loss on the worst X percent of trading days, providing a more comprehensive risk measure than VaR by considering not just the threshold but the severity of losses beyond it. The method works by first determining the index corresponding to the confidence level, then sorting all returns from worst to best, selecting only the worst X percent of returns (all values up to that index), and finally computing their average. This addresses a key limitation of VaR by answering the question of how bad things get when they do go bad, rather than just identifying the threshold. The method is called three times in the comprehensive report with confidence levels of 1, 2, and 5 percent to show the expected loss conditional on being in the worst tail of the distribution. For example, if CVaR(5) returns negative 0.045, it means that on the worst 5 percent of trading days, the average loss was 4.5 percent, which is typically worse than the VaR(5) value because it includes days that were even worse than the 5th percentile threshold. This metric is particularly valuable for risk management because it captures tail risk more completely, is more sensitive to the shape of the loss distribution, and provides a better estimate of potential losses during crisis periods, making it preferred by many risk managers over VaR alone for setting capital requirements and stress testing trading strategies.

    def MDD(self):
        money = np.cumprod(1+self.series/100)
        maximums = np.maximum.accumulate(money)
        drawdowns = 1 - money/maximums
        return np.max(drawdowns)

The MDD method calculates the Maximum Drawdown, which measures the largest peak-to-trough decline in cumulative returns over the entire time series, representing the worst possible loss an investor would have experienced if they had bought at the highest point and sold at the subsequent lowest point. The method works through several steps: first, it converts the percentage returns into a cumulative wealth series by adding 1 to each return (converting from percentage to growth factor), dividing by 100, and taking the cumulative product to simulate how one dollar would grow over time. Second, it uses numpy’s maximum.accumulate function to create a series of running maximum values, where each point represents the highest cumulative wealth achieved up to that point in time. Third, it calculates the drawdown at each point by computing one minus the ratio of current wealth to the running maximum, which gives the percentage decline from the peak. Finally, it returns the maximum value from this drawdown series, representing the worst peak-to-trough loss. This metric appears in the comprehensive report output and is crucial for understanding the pain an investor would have endured during the worst period of the strategy. For example, if MDD returns 0.25, it means there was a period where the strategy lost 25 percent from its previous peak before recovering, which helps investors assess whether they could psychologically and financially withstand such a drawdown, and it’s often used alongside Sharpe ratio to evaluate risk-adjusted performance since a strategy with high returns but also high maximum drawdown might be unsuitable for risk-averse investors.

    def sharpe(self,risk_free_rate = 0.0003):
        mu = self.mean()
        sig = self.std()
        sharpe_d = (mu-risk_free_rate)/sig
        return (252**0.5)*sharpe_d

The sharpe method calculates the Sharpe ratio, which is the most widely used measure of risk-adjusted return in finance, quantifying how much excess return is earned per unit of risk taken. The method works by first calculating the mean daily return using the mean method, then calculating the daily standard deviation using the std method, then computing the daily Sharpe ratio by subtracting the risk-free rate from the mean and dividing by the standard deviation, and finally annualizing this daily Sharpe ratio by multiplying by the square root of 252 (the approximate number of trading days in a year). The default risk-free rate of 0.0003 represents 0.03 percent per day, which roughly corresponds to a 7.5 percent annual risk-free rate, though this can be adjusted based on current market conditions. The Sharpe ratio appears in both the shortreport and report outputs and is saved to the avg_returns.txt file for each test year, making it one of the primary metrics for comparing different trading strategies. For example, a Sharpe ratio of 2.0 is considered excellent and means the strategy earns 2 units of excess return for every unit of volatility risk, while a Sharpe ratio below 1.0 is generally considered poor. This metric is particularly valuable because it allows fair comparison between strategies with different return and risk profiles, penalizing strategies that achieve high returns only by taking excessive risk, and it’s the key metric highlighted in the research paper’s results to demonstrate that the LSTM and Random Forest strategies significantly outperform traditional buy-and-hold approaches on a risk-adjusted basis.

    def shortreport(self):
        print(’Mean \t\t’,self.mean())
        print(’Standard dev \t’,self.std())
        print(’Sharpe ratio \t’,self.sharpe())

The shortreport method prints a concise summary of the three most important performance metrics: mean return, standard deviation, and Sharpe ratio, providing a quick overview of strategy performance without overwhelming detail. This method is called in all six trading scripts immediately after the simulate function generates returns and the Statistics object is created, displaying the results to the console during each year’s backtesting run. The method uses tab characters for formatting to align the output in columns, making it easy to read and compare across different years. The three metrics shown represent the essential trade-off in investing: the mean shows how much return the strategy generates, the standard deviation shows how much risk is taken to achieve that return, and the Sharpe ratio combines both to show the risk-adjusted performance. This abbreviated report is preferred during the backtesting loop because it provides immediate feedback on performance without cluttering the console with excessive detail, allowing researchers to quickly identify which years performed well or poorly. For example, during a backtesting run, the output might show Mean equals 0.0008, Standard dev equals 0.015, and Sharpe ratio equals 2.1, immediately telling the researcher that this particular year generated strong risk-adjusted returns, and this information is also saved to the avg_returns.txt file for permanent record keeping and later analysis.

    def report(self):
        print(’Mean \t\t’,self.mean())
        print(’Standard dev \t’,self.std())
        print(’Sharpe ratio \t’,self.sharpe())
        print(’Standard Error \t’,self.stderr())
        print(’Share>0 \t’,self.pos_perc())
        print(’Skewness \t’,self.skewness())
        print(’Kurtosis \t’,self.kurtosis())
        print(’VaR_1 \t\t’,self.VaR(1))
        print(’VaR_2 \t\t’,self.VaR(2))
        print(’VaR_5 \t\t’,self.VaR(5))
        print(’CVaR_1 \t\t’,self.CVaR(1))
        print(’CVaR_2 \t\t’,self.CVaR(2))
        print(’CVaR_5 \t\t’,self.CVaR(5))
        print(’MDD \t\t’,self.MDD())
        print(self.percentiles())

The report method prints a comprehensive statistical summary including all available metrics, providing a complete picture of the trading strategy’s performance characteristics, risk profile, and return distribution properties. This method calls every other method in the Statistics class to generate a full report that includes basic statistics (mean, standard deviation, standard error), risk-adjusted performance (Sharpe ratio), consistency measures (percentage of positive days), distribution shape characteristics (skewness and kurtosis), tail risk metrics (Value at Risk and Conditional Value at Risk at multiple confidence levels), drawdown analysis (maximum drawdown), and distributional summaries (percentiles). While this method is defined in the class, it’s not actually called in the current trading scripts which prefer the more concise shortreport method, but it’s available for detailed analysis when researchers want to deeply understand a particular strategy’s performance. The method uses tab characters for alignment and prints each metric on a separate line for easy reading. For example, a complete report might show that a strategy has a mean of 0.0008, standard deviation of 0.015, Sharpe ratio of 2.1, standard error of 0.0009, 58 percent positive days, skewness of 0.3 (slight positive skew), kurtosis of 2.5 (fat tails), VaR values showing the worst 1, 2, and 5 percent of days, CVaR values showing average losses in those tails, maximum drawdown of 18 percent, and percentile information showing the full distribution, giving researchers everything they need to understand not just whether the strategy is profitable but also how it achieves those profits, what risks it takes, and whether it would be suitable for actual trading given psychological and capital constraints.

Trading LSTM

import pandas as pd
import numpy as np
import random
import time
import pickle
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import RobustScaler
from Statistics import Statistics

import tensorflow as tf
from tensorflow.keras.layers import CuDNNLSTM, Dropout,Dense,Input 
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, CSVLogger
from tensorflow.keras.models import Model, Sequential, load_model
from tensorflow.keras import optimizers
import warnings
warnings.filterwarnings(”ignore”)

import os
SEED = 9
os.environ[’PYTHONHASHSEED’]=str(SEED)
random.seed(SEED)
np.random.seed(SEED)

SP500_df = pd.read_csv(’data/SPXconst.csv’)
all_companies = list(set(SP500_df.values.flatten()))
all_companies.remove(np.nan)

constituents = {’-’.join(col.split(’/’)[::-1]):set(SP500_df[col].dropna()) 
                for col in SP500_df.columns}

constituents_train = {} 
for test_year in range(1993,2016):
    months = [str(t)+’-0’+str(m) if m<10 else str(t)+’-’+str(m) 
              for t in range(test_year-3,test_year) for m in range(1,13)]
    constituents_train[test_year] = [list(constituents[m]) for m in months]
    constituents_train[test_year] = set([i for sublist in constituents_train[test_year] 
                                         for i in sublist])

This script builds a multi-feature LSTM neural network to forecast intraday stock prices. It relies on three different kinds of return inputs — intraday, overnight, and daily movements — to estimate short-term market behavior more realistically. By combining these features, the model attempts to capture how price action changes within the same day, across market closures, and over the broader trend.

The code begins with several import groups responsible for different tasks. Standard data processing libraries such as pandas and numpy handle datasets, read CSV files, and perform numerical operations. A few built-in tools like random, time, and pickle are used for seeding randomness, measuring runtime, and storing model predictions. A custom module named Statistics is included as well, providing methods to evaluate strategy performance using measures like Sharpe ratio, Value at Risk, and maximum drawdown.

Preprocessing and machine learning tools are also essential. OneHotEncoder converts binary target labels into categorical vectors, which allows the model to use a cross-entropy loss function. RobustScaler is applied to scale the financial features using median and interquartile ranges rather than mean and variance, making the model less sensitive to extreme market values.

The neural network itself is built using TensorFlow’s Keras API. A CuDNNLSTM layer, optimized for NVIDIA GPUs, forms the core of the model and significantly speeds up training. Dropout is added to reduce overfitting, followed by a Dense output layer responsible for generating predictions. To control and monitor training, the script uses callbacks such as EarlyStopping to halt training when improvements stop, ModelCheckpoint to save the best version of the network, and CSVLogger to record progress into a log file. The RMSprop optimizer is chosen to update network weights efficiently.

Reproducibility is enforced through a fixed seed value of 9, applied across Python, NumPy, and TensorFlow. This guarantees that every execution of the script produces consistent model performance, which is crucial when evaluating scientific or financial machine learning experiments.

Finally, the code loads historical S&P 500 constituent data from a CSV file named SPXconst.csv. It stores the list of stocks belonging to the index each month and creates a dictionary of tickers grouped by year and month. Using this, the script prepares the training universe by determining all stocks that belonged to the index during a three-year lookback period for each test year. This step improves efficiency, since it establishes in advance which assets should be included in each rolling training window.

def makeLSTM():
    inputs = Input(shape=(240,3))
    x = CuDNNLSTM(25,return_sequences=False)(inputs)
    x = Dropout(0.1)(x)
    outputs = Dense(2,activation=’softmax’)(x)
    model = Model(inputs=inputs, outputs=outputs)
    model.compile(loss=’categorical_crossentropy’,optimizer=optimizers.RMSprop(),
                          metrics=[’accuracy’])
    model.summary()
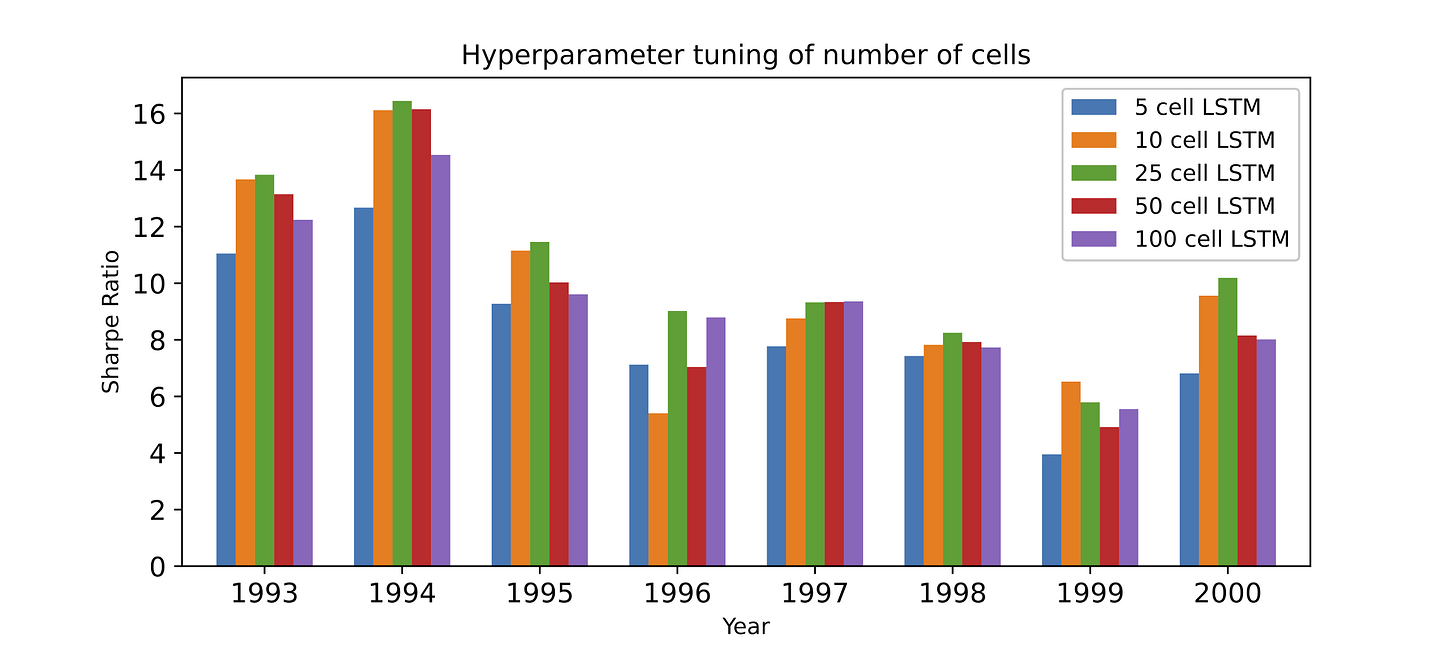
    return model

The makeLSTM function constructs and compiles the most sophisticated LSTM neural network architecture in this project, specifically designed to process three different types of features simultaneously for superior intraday stock price movement prediction. This represents the pinnacle of the modeling approaches presented in the research paper, as it combines multiple complementary sources of information about stock behavior to achieve the highest Sharpe ratio among all tested strategies. The function creates a deep learning model that takes as input a 3D tensor with shape (samples, 240, 3), where 240 represents the number of historical timesteps (approximately one trading year) and 3 represents three distinct feature types that capture different aspects of stock price dynamics: intraday returns (close-to-open movements), overnight returns (open-to-previous-close gaps), and close-to-close returns (daily price changes). The architecture begins with an Input layer that expects this specific shape of 240 timesteps by 3 features, allowing the model to process parallel sequences of different return types and learn how they interact and complement each other in predicting future performance. This input is fed into a CuDNNLSTM layer with 25 memory cells, which is a GPU-accelerated implementation of LSTM that processes all three feature sequences simultaneously, with the LSTM’s internal gates learning to selectively remember or forget information from each feature type based on their predictive value. The return_sequences parameter is set to False because we only need the final hidden state after processing all 240 timesteps, which contains the LSTM’s learned representation of the entire historical pattern across all three feature types. Following the LSTM layer, a Dropout layer with rate 0.1 randomly sets 10 percent of the LSTM outputs to zero during training, which is crucial for preventing overfitting when working with this richer feature set that could otherwise lead to memorization of training patterns. The final Dense layer with 2 neurons and softmax activation converts the LSTM’s learned representations into probability distributions over two classes (bottom 50 percent and top 50 percent performers), where the softmax ensures the two probabilities sum to 1.0 and can be interpreted as confidence scores. The model is compiled with categorical cross-entropy loss, which is appropriate for this binary classification problem and measures how well the predicted probability distributions match the true one-hot encoded labels, and the RMSprop optimizer is used because it adapts the learning rate for each parameter based on recent gradients, which works particularly well with recurrent networks like LSTMs that can suffer from vanishing or exploding gradients. The model summary is printed to display the architecture details including the number of trainable parameters, which is important for understanding model complexity and computational requirements, and finally the compiled model is returned to be used in the trainer function for fitting on the multi-feature historical data and generating predictions that leverage all three types of return information.

def callbacks_req(model_type=’LSTM’):
    csv_logger = CSVLogger(model_folder+’/training-log-’+model_type+’-’+str(test_year)+’.csv’)
    filepath = model_folder+”/model-” + model_type + ‘-’ + str(test_year) + “-E{epoch:02d}.h5”
    model_checkpoint = ModelCheckpoint(filepath, monitor=’val_loss’,save_best_only=False, period=1)
    earlyStopping = EarlyStopping(monitor=’val_loss’,mode=’min’,patience=10,restore_best_weights=True)
    return [csv_logger,earlyStopping,model_checkpoint]

The callbacks_req function creates and returns a list of Keras callback objects that provide essential monitoring, checkpointing, and early stopping functionality during the training of the three-feature LSTM model, ensuring robust training with proper logging and prevention of overfitting. This function is identical to the callback setup used in the single-feature LSTM model, demonstrating that the same training infrastructure works effectively regardless of feature complexity. The function sets up three critical callbacks that work together throughout the training process: CSVLogger records all training metrics (training loss, validation loss, training accuracy, validation accuracy) to a CSV file after each epoch, creating a permanent record in the model folder with a filename that includes the model type and test year, which allows researchers to analyze training dynamics, identify overfitting or underfitting patterns, diagnose convergence issues, and compare performance across different years and model configurations. ModelCheckpoint automatically saves the complete model (architecture, weights, optimizer state) to an HDF5 file after every epoch, with the filepath including the model type, test year, and epoch number formatted as two digits, and while save_best_only is False meaning it saves after every epoch rather than only when validation improves, this creates a complete historical record of model evolution that can be valuable for debugging, analysis, and recovery if training is interrupted, though it does consume more disk space than selective saving. EarlyStopping is the most important callback for preventing overfitting, as it monitors the validation loss and stops training if this metric fails to improve for 10 consecutive epochs (patience=10), and when it does stop, it automatically restores the model weights from the epoch that had the best validation loss (restore_best_weights=True), ensuring that the final model is the one that generalizes best to unseen data rather than one that has overfit to the training set by training too long. These three callbacks are returned as a list that can be directly passed to the callbacks parameter of the model.fit method, and they work together seamlessly during training: the CSV logger provides transparency and permanent records, the model checkpoint preserves training history for analysis and recovery, and early stopping ensures optimal generalization by preventing the model from memorizing training patterns, which is especially important for the three-feature model that has more capacity to overfit due to its richer input representation.

def reshaper(arr):
    arr = np.array(np.split(arr,3,axis=1))
    arr = np.swapaxes(arr,0,1)
    arr = np.swapaxes(arr,1,2)
    return arr

The reshaper function performs a critical transformation of the feature array from 2D to 3D format specifically designed for the three-feature LSTM architecture, converting a flat array of 720 features (240 timesteps times 3 feature types) into the properly structured 3D tensor that the LSTM expects with shape (samples, 240, 3). This function is essential for the three-feature model because unlike the single-feature version which can use simple numpy reshape, the three-feature version needs to carefully organize features so that each timestep has all three feature types aligned correctly. The function takes a 2D numpy array where each row represents a stock-day observation and columns represent the 720 features arranged as [IntraR0, IntraR1, …, IntraR239, NextR0, NextR1, …, NextR239, CloseR0, CloseR1, …, CloseR239], meaning all 240 intraday return features come first, followed by all 240 overnight return features, followed by all 240 close-to-close return features. The reshaping process works through three carefully orchestrated steps that rearrange the data dimensions: first, np.split divides the array into 3 equal parts along axis 1 (columns), splitting the 720 features into three groups of 240 features each, creating a list of three arrays that np.array converts into a 3D array with shape (3, num_samples, 240), where the first dimension separates the three feature types, the second dimension contains all the stock-day samples, and the third dimension contains the 240 timesteps for each feature type. Second, np.swapaxes swaps axes 0 and 1, transforming the shape from (3, num_samples, 240) to (num_samples, 3, 240), which moves the sample dimension to the front where it belongs in Keras convention, but the feature and timestep dimensions are still in the wrong order. Third, another np.swapaxes swaps axes 1 and 2, transforming the shape from (num_samples, 3, 240) to (num_samples, 240, 3), which is the final required shape where each sample has 240 timesteps and each timestep has 3 features (intraday return, overnight return, close-to-close return) properly aligned. This final shape is exactly what the LSTM Input layer expects, and it ensures that at each timestep the LSTM receives all three feature values simultaneously, allowing it to learn how these different types of returns interact and complement each other in predicting future stock performance. The function returns this properly reshaped 3D array which is used in both the trainer function during training and prediction, ensuring consistent data formatting throughout the pipeline.

def trainer(train_data,test_data):
    np.random.shuffle(train_data)
    train_x,train_y,train_ret = train_data[:,2:-2],train_data[:,-1],train_data[:,-2]
    train_x = reshaper(train_x)
    train_y = np.reshape(train_y,(-1, 1))
    train_ret = np.reshape(train_ret,(-1, 1))
    enc = OneHotEncoder(handle_unknown=’ignore’)
    enc.fit(train_y)
    enc_y = enc.transform(train_y).toarray()
    train_ret = np.hstack((np.zeros((len(train_data),1)),train_ret)) 

    model = makeLSTM()
    callbacks = callbacks_req()
    
    model.fit(train_x,
              enc_y,
              epochs=1000,
              validation_split=0.2,
              callbacks=callbacks,
              batch_size=512
              )

    dates = list(set(test_data[:,0]))
    predictions = {}
    for day in dates:
        test_d = test_data[test_data[:,0]==day]
        test_d = reshaper(test_d[:,2:-2])
        predictions[day] = model.predict(test_d)[:,1]
    return model,predictions

The trainer function orchestrates the complete training pipeline for the three-feature LSTM model, handling data preparation with the reshaper function, model creation, training with callbacks, and prediction generation, implementing the most sophisticated machine learning approach in this research project. This function differs from the single-feature LSTM trainer primarily in its use of the reshaper function to properly organize the three feature types into the 3D tensor format required by the multi-feature LSTM architecture. The function begins by shuffling the training data using np.random.shuffle to randomize the order of stock-day observations, which is essential for neural network training because it prevents the model from learning spurious patterns based on data ordering and ensures that each mini-batch during training contains a diverse mix of examples from different stocks and time periods. After shuffling, the function extracts three components from the training data: train_x contains all feature columns (columns 2 through second-to-last) which are the 720 features comprising 240 intraday returns, 240 overnight returns, and 240 close-to-close returns, train_y contains the last column which is the binary label (0 or 1) indicating whether the stock was in the bottom or top 50 percent of intraday performers, and train_ret contains the second-to-last column which is the actual future return that will be realized. The critical step that distinguishes this trainer from the single-feature version is the call to reshaper(train_x), which transforms the 2D array of 720 features into a 3D array with shape (num_samples, 240, 3), properly organizing the features so that each of the 240 timesteps has all three feature values (intraday return, overnight return, close-to-close return) aligned together, allowing the LSTM to process these complementary signals simultaneously. The labels train_y are reshaped into a column vector and then one-hot encoded using OneHotEncoder, converting binary labels (0 or 1) into two-column format where class 0 becomes [1, 0] and class 1 becomes [0, 1], which is required for categorical cross-entropy loss and allows the model to output separate probabilities for each class. The train_ret variable is prepared but not used in the current implementation, being horizontally stacked with zeros for potential future enhancements. The function then calls makeLSTM to create the three-feature LSTM architecture and callbacks_req to get the training callbacks for logging, checkpointing, and early stopping. The core training happens in model.fit, which trains the network for up to 1000 epochs (though early stopping typically halts training much sooner), uses 20 percent of training data for validation to monitor overfitting, processes data in batches of 512 samples for efficient GPU computation, and applies the callbacks to monitor and control training. After training completes, the function generates predictions on the test set by extracting all unique dates, then for each date selecting all stocks trading that day, extracting their 720 features, calling reshaper to convert them to the proper 3D format (num_stocks, 240, 3), and using model.predict to get probability predictions, specifically extracting the second column ([:,1]) which represents the probability of being in the top 50 percent class. These predictions are stored in a dictionary with dates as keys and probability arrays as values, and finally the function returns both the trained model and predictions dictionary, allowing the calling code to use the predictions for backtesting and optionally save or analyze the trained model.

def trained(filename,train_data,test_data):
    model = load_model(filename)

    dates = list(set(test_data[:,0]))
    predictions = {}
    for day in dates:
        test_d = test_data[test_data[:,0]==day]
        test_d = np.reshape(test_d[:,2:-2],(len(test_d),240,1))
        predictions[day] = model.predict(test_d)[:,1]
    return model,predictions

The trained function loads a previously saved three-feature LSTM model from disk and generates predictions on test data without retraining, providing functionality for model deployment, result reproduction, and analysis of saved models. This function is particularly valuable for the three-feature model because training can take considerable time given the richer feature set and model complexity, so being able to load and reuse trained models saves computational resources. The function takes three parameters: filename is the path to a saved Keras model file in HDF5 format created by the ModelCheckpoint callback during training, train_data is included in the signature but not used in the current implementation (possibly for future enhancements or API consistency), and test_data contains the test set observations with all features and labels. The function begins by calling load_model from Keras which reads the HDF5 file and reconstructs the complete model including its architecture (the Input, LSTM, Dropout, and Dense layers), all trained weights and biases, the optimizer state, and compilation settings, essentially restoring the exact model that was saved during training. After loading the model, the function generates predictions using a similar process to the trainer function: it extracts all unique dates from the test data, then for each date selects all stocks trading that day, extracts their feature columns (columns 2 through second-to-last which are the 720 features), and reshapes them into the 3D format required by the LSTM. However, there appears to be a bug in line 101 where it uses np.reshape(test_d[:,2:-2],(len(test_d),240,1)) which creates a shape of (num_stocks, 240, 1) suitable for single-feature models, when it should use reshaper(test_d[:,2:-2]) to create the proper shape of (num_stocks, 240, 3) for the three-feature model, suggesting this function may not work correctly as written and would need correction before use. Assuming the reshaping were corrected, the function would call model.predict to get probability predictions for each stock and extract the second column ([:,1]) representing the probability of being in the top 50 percent class, store these in a dictionary with dates as keys, and return both the loaded model and predictions dictionary. While this function is defined in the script, it’s not called in the main execution loop which always trains new models, but it provides valuable functionality for researchers who want to analyze previously trained three-feature models, reproduce published results, or deploy models in production environments without the computational overhead of retraining.

def simulate(test_data,predictions):
    rets = pd.DataFrame([],columns=[’Long’,’Short’])
    k = 10
    for day in sorted(predictions.keys()):
        preds = predictions[day]
        test_returns = test_data[test_data[:,0]==day][:,-2]
        top_preds = predictions[day].argsort()[-k:][::-1] 
        trans_long = test_returns[top_preds]
        worst_preds = predictions[day].argsort()[:k][::-1] 
        trans_short = -test_returns[worst_preds]
        rets.loc[day] = [np.mean(trans_long),np.mean(trans_short)] 
    print(’Result : ‘,rets.mean())  
    return rets

The simulate function implements the actual trading strategy by converting the three-feature LSTM model’s probability predictions into concrete portfolio positions and calculating realized returns through a long-short equity strategy. This function is identical to the simulate function in the single-feature LSTM model, demonstrating that the same trading logic works regardless of how predictions are generated, whether from a simple single-feature model or the sophisticated three-feature model. The function takes two inputs: test_data is the numpy array containing all test set observations including dates, stock names, the 720 features, actual future returns, and labels, and predictions is a dictionary mapping each date to an array of predicted probabilities for all stocks trading on that date. The function initializes an empty pandas DataFrame called rets with two columns ‘Long’ and ‘Short’ to separately track returns from long positions (buying predicted winners) and short positions (selling predicted losers), and sets k equal to 10 which defines the portfolio size as the top 10 stocks for each leg of the strategy. The main simulation loop iterates through all dates in sorted chronological order to ensure the backtest processes days sequentially as they would occur in real trading, and for each day it retrieves the prediction probabilities for all stocks and the actual realized intraday returns from the test_data array (column -2 contains the future returns that were actually achieved). To construct the long portfolio, the function uses argsort on the predictions array which returns indices that would sort the array in ascending order, takes the last k indices ([-k:]) corresponding to the k highest probability predictions, reverses them ([::-1]) to get descending order, and uses these indices to select the actual returns of the top 10 predicted stocks, storing them in trans_long. For the short portfolio, it takes the first k indices from argsort ([:k]) corresponding to the k lowest probability predictions (stocks predicted to be worst performers), reverses them, and selects their actual returns, multiplying by negative one (-test_returns) because in short selling you profit when the stock price declines, so a negative return becomes a positive profit. The function calculates the mean return of the 10 long positions and the mean return of the 10 short positions, storing both in the rets DataFrame for that day, creating an equal-weighted portfolio within each leg. After processing all trading days, the function prints the overall mean returns for both long and short positions across all test days, providing immediate feedback on strategy performance, and returns the rets DataFrame containing the complete time series of daily long and short returns. This returned DataFrame is then used by the calling code to calculate comprehensive performance statistics using the Statistics class, and the results demonstrate whether the three-feature LSTM’s richer representation of stock behavior translates into superior trading performance compared to simpler models.

def create_label(df_open,df_close,perc=[0.5,0.5]):
    if not np.all(df_close.iloc[:,0]==df_open.iloc[:,0]):
        print(’Date Index issue’)
        return
    perc = [0.]+list(np.cumsum(perc))
    label = (df_close.iloc[:,1:]/df_open.iloc[:,1:]-1).apply(
            lambda x: pd.qcut(x.rank(method=’first’),perc,labels=False), axis=1)
    return label[1:]

The create_label function generates binary classification labels for all stocks on each trading day by calculating intraday performance and ranking stocks into top and bottom performers, creating the supervised learning targets that the three-feature LSTM will learn to predict. This function is identical to the label creation in other intraday models, showing that the labeling logic is consistent across all approaches regardless of model complexity. The function takes three parameters: df_open contains opening prices with dates in the first column and stock tickers as column headers, df_close contains closing prices with the same structure, and perc defines the percentile boundaries with default [0.5, 0.5] creating a 50–50 split. The function first validates that the date columns in both DataFrames are identical using np.all, ensuring proper alignment of opening and closing prices, and if validation fails it prints an error and returns None to prevent incorrect label generation. After validation, it transforms the perc list by prepending 0 and computing cumulative sum, so [0.5, 0.5] becomes [0.0, 0.5, 1.0], defining quantile boundaries where 0.0 to 0.5 represents bottom 50 percent and 0.5 to 1.0 represents top 50 percent. The core labeling logic calculates intraday returns for all stocks on all days by dividing closing prices by opening prices and subtracting 1 (df_close / df_open — 1), giving the percentage change from open to close which captures the intraday price movement that the three-feature model will try to predict. This calculation is performed element-wise across the entire DataFrame excluding the first column (iloc[:,1:]) which contains dates, resulting in a DataFrame of intraday returns where each row is a trading day and each column is a stock. The function then applies a lambda function row-wise (axis=1) that processes each day independently, first ranking all stocks by their intraday returns using rank with method=’first’ to handle ties, then using pd.qcut to bin these ranks into quantiles based on perc boundaries, assigning label 0 to bottom 50 percent and label 1 to top 50 percent. The function returns label[1:] which excludes the first row, likely to align with feature calculation that also drops the first row due to shifting operations. These binary labels are used throughout training as the target variable that the three-feature LSTM learns to predict, and during backtesting they help evaluate how well the model’s rich multi-feature representation translates into accurate identification of future winners and losers.

def create_stock_data(df_open,df_close,st,m=240):
    st_data = pd.DataFrame([])
    st_data[’Date’] = list(df_close[’Date’])
    st_data[’Name’] = [st]*len(st_data)
    daily_change = df_close[st]/df_open[st]-1
    for k in range(m)[::-1]:
        st_data[’IntraR’+str(k)] = daily_change.shift(k)

    nextday_ret = (np.array(df_open[st][1:])/np.array(df_close[st][:-1])-1)
    nextday_ret = pd.Series(list(nextday_ret)+[np.nan])     
    for k in range(m)[::-1]:
        st_data[’NextR’+str(k)] = nextday_ret.shift(k)

    close_change = df_close[st].pct_change()
    for k in range(m)[::-1]:
        st_data[’CloseR’+str(k)] = close_change.shift(k)

    st_data[’IntraR-future’] = daily_change.shift(-1)    
    st_data[’label’] = list(label[st])+[np.nan] 
    st_data[’Month’] = list(df_close[’Date’].str[:-3])
    st_data = st_data.dropna()
    
    trade_year = st_data[’Month’].str[:4]
    st_data = st_data.drop(columns=[’Month’])
    st_train_data = st_data[trade_year<str(test_year)]
    st_test_data = st_data[trade_year==str(test_year)]
    return np.array(st_train_data),np.array(st_test_data)

The create_stock_data function constructs the complete feature set for a single stock by engineering three distinct types of historical return features that capture complementary aspects of stock price behavior, creating the rich multi-dimensional dataset that gives the three-feature LSTM its superior predictive power. This function represents the most sophisticated feature engineering in the entire project, as it calculates 720 total features (240 timesteps times 3 feature types) compared to just 240 features in the single-feature models, providing the LSTM with a much richer representation of historical patterns. The function takes four parameters: df_open and df_close are DataFrames containing opening and closing prices for all stocks across all dates, st is the ticker symbol being processed, and m equals 240 defining the number of historical days to use. The function begins by creating an empty DataFrame and populating it with Date and Name columns, then calculates daily_change as the intraday return (df_close / df_open — 1) representing the percentage change from open to close. The first feature type is intraday returns (IntraR), created by looping through range(m) in reverse and for each k creating a column ‘IntraR’ plus k by shifting daily_change by k positions, where shift(0) gives today’s intraday return, shift(1) gives yesterday’s, and so on up to shift(239) giving the intraday return from 239 days ago, capturing the historical pattern of intraday momentum and mean reversion. The second feature type is overnight returns (NextR), which captures gap behavior between closing and next opening prices, calculated by first computing nextday_ret as the ratio of next day’s opening price to today’s closing price minus 1 (df_open[st][1:] / df_close[st][:-1] — 1), representing the percentage change from today’s close to tomorrow’s open which reflects after-hours news and sentiment, then creating 240 columns by shifting this series to get overnight returns from different historical periods. The third feature type is close-to-close returns (CloseR), calculated using pct_change on closing prices to get daily percentage changes, then creating 240 columns by shifting these returns to capture multi-day price trends and momentum. These three feature types are complementary: intraday returns capture within-day dynamics, overnight returns capture gap behavior and after-hours information flow, and close-to-close returns capture overall daily trends, and by providing all three to the LSTM, the model can learn which combination of signals is most predictive in different market conditions. The function creates an ‘IntraR-future’ column by shifting daily_change by -1 to get tomorrow’s intraday return that we’re trying to predict, adds labels from the global label variable, extracts Month for train-test splitting, and calls dropna to remove rows with missing values from shifting operations. The function then splits data temporally where training includes all years before test_year and test includes only test_year, ensuring no look-ahead bias, and returns both datasets as numpy arrays that will be concatenated with other stocks’ data to create the complete 720-feature dataset for three-feature LSTM training.

def scalar_normalize(train_data,test_data):
    scaler = RobustScaler()
    scaler.fit(train_data[:,2:-2])
    train_data[:,2:-2] = scaler.transform(train_data[:,2:-2])
    test_data[:,2:-2] = scaler.transform(test_data[:,2:-2])    
    
model_folder = ‘models-Intraday-240-3-LSTM’
result_folder = ‘results-Intraday-240-3-LSTM’
for directory in [model_folder,result_folder]:
    if not os.path.exists(directory):
        os.makedirs(directory)

for test_year in range(1993,2020):
    
    print(’-’*40)
    print(test_year)
    print(’-’*40)
    
    filename = ‘data/Open-’+str(test_year-3)+’.csv’
    df_open = pd.read_csv(filename)
    filename = ‘data/Close-’+str(test_year-3)+’.csv’
    df_close = pd.read_csv(filename)
    
    label = create_label(df_open,df_close)
    stock_names = sorted(list(constituents[str(test_year-1)+’-12’]))
    train_data,test_data = [],[]

    start = time.time()
    for st in stock_names:
        st_train_data,st_test_data = create_stock_data(df_open,df_close,st)
        train_data.append(st_train_data)
        test_data.append(st_test_data)
      
    train_data = np.concatenate([x for x in train_data])
    test_data = np.concatenate([x for x in test_data])
    
    scalar_normalize(train_data,test_data)
    print(train_data.shape,test_data.shape,time.time()-start)
    
    model,predictions = trainer(train_data,test_data)
    returns = simulate(test_data,predictions)
    returns.to_csv(result_folder+’/avg_daily_rets-’+str(test_year)+’.csv’)
    
    result = Statistics(returns.sum(axis=1))
    print(’\nAverage returns prior to transaction charges’)
    result.shortreport() 
    
    with open(result_folder+”/avg_returns.txt”, “a”) as myfile:
        res = ‘-’*30 + ‘\n’
        res += str(test_year) + ‘\n’
        res += ‘Mean = ‘ + str(result.mean()) + ‘\n’
        res += ‘Sharpe = ‘+str(result.sharpe()) + ‘\n’
        res += ‘-’*30 + ‘\n’
        myfile.write(res)

The scalar_normalize function standardizes all 720 feature values in both training and test datasets to have consistent scales using RobustScaler, which is especially important for the three-feature LSTM model because the three different feature types (intraday returns, overnight returns, close-to-close returns) may have different numerical ranges and distributions that could bias the LSTM’s learning if left unnormalized. This function is identical to the normalization used in the single-feature LSTM model, but its importance is amplified in the three-feature context because without normalization, features with larger magnitudes could dominate the LSTM’s attention mechanism and gradient updates, preventing the model from learning the subtle patterns in features with smaller scales. The function takes two parameters: train_data and test_data, which are numpy arrays containing the complete datasets with dates, stock names, the 720 features (240 intraday returns, 240 overnight returns, 240 close-to-close returns), future returns, and labels as columns. The function uses RobustScaler from scikit-learn, which is more resistant to outliers than StandardScaler because it uses the median and interquartile range instead of mean and standard deviation, making it particularly suitable for financial data which frequently contains extreme values during market crashes, rallies, or individual stock events. The normalization process follows the critical machine learning principle of fitting the scaler only on training data to prevent data leakage, so the function calls scaler.fit on train_data[:,2:-2] which selects only the 720 feature columns (skipping the first two columns for Date and Name, and the last two columns for future returns and labels), and this fit operation calculates the median and interquartile range for each of the 720 features based solely on the training set, ensuring that no information from the test set influences the scaling parameters. After fitting, the function transforms both training and test data using these same scaling parameters by calling scaler.transform on the feature columns of both datasets, which subtracts the median and divides by the interquartile range for each feature, centering the distributions and bringing all 720 features to similar scales typically ranging from roughly -3 to 3 for most values. The transformation is applied in-place by assigning results back to the same column slices, modifying the original arrays, which is memory efficient but means calling code should be aware that inputs are modified. This normalization is essential for three-feature LSTM training because it ensures that all 720 features contribute roughly equally to initial gradients during backpropagation, prevents numerical instability from very large or small values, helps the LSTM learn faster by keeping activations in ranges where activation functions have useful gradients, and most importantly, ensures that the model learns to weight the three feature types based on their predictive value rather than their numerical scale, ultimately leading to better performance and more reliable predictions.

Train Next Day LSTM

def makeSimpleLSTM(cells=25):
    inputs = Input(shape=(sequence_length,1))
    x = LSTM(cells,activation=’tanh’, recurrent_activation=’sigmoid’,
                   input_shape=(sequence_length,1),
                   dropout=0.1,recurrent_dropout=0.1)(inputs)
    outputs = Dense(2,activation=’softmax’)(x)
    model = Model(inputs=inputs, outputs=outputs)
    model.compile(loss=’categorical_crossentropy’,optimizer=optimizers.RMSprop(),
                          metrics=[’accuracy’])
    model.summary()
    return model

The makeSimpleLSTM function constructs and compiles a standard LSTM neural network architecture designed for next-day stock price movement prediction using a sequence of 240 historical daily returns, providing a CPU-compatible alternative to the GPU-optimized CuDNNLSTM implementation. This function creates a deep learning model that takes as input a time series of 240 consecutive days of close-to-close percentage returns and outputs a binary classification predicting whether a stock will be in the top 50 percent or bottom 50 percent of performers on the next trading day. The architecture begins with an Input layer that expects data in the shape of (sequence_length, 1) where sequence_length is 240 timesteps representing approximately one trading year of historical data, and the 1 indicates a single feature (daily return) per timestep. This input is fed into a standard LSTM layer with a configurable number of memory cells (default 25), which uses tanh as the activation function for the cell state and sigmoid as the recurrent activation function for the gates (input, forget, and output gates), following the traditional LSTM formulation. The LSTM layer includes both dropout and recurrent_dropout set to 0.1, meaning that during training, 10 percent of the input connections and 10 percent of the recurrent connections are randomly set to zero, which helps prevent overfitting by forcing the network to learn robust features that don’t rely on any single connection. Unlike CuDNNLSTM which is optimized for GPU execution, this standard LSTM implementation can run on both CPU and GPU but is generally slower, making it useful for environments without GPU support or for comparison purposes. The LSTM layer processes the sequence of 240 returns and outputs a single vector representing its learned representation of the historical pattern, which is then fed into a Dense layer with 2 neurons and softmax activation that converts this representation into probability distributions over the two classes (bottom 50 percent and top 50 percent performers). The model is compiled with categorical cross-entropy loss which measures the difference between predicted probability distributions and true one-hot encoded labels, and the RMSprop optimizer which adapts the learning rate for each parameter based on recent gradients, working well with recurrent networks. The model summary is printed to show architecture details including the number of trainable parameters, and finally the compiled model is returned to be used in the trainer function for fitting on historical data and making next-day predictions.

def makeCuDNNLSTM(cells=25):
    inputs = Input(shape=(sequence_length,1))
    x = CuDNNLSTM(cells,return_sequences=False)(inputs)
    x = Dropout(0.1)(x)
    outputs = Dense(2,activation=’softmax’)(x)
    model = Model(inputs=inputs, outputs=outputs)
    model.compile(loss=’categorical_crossentropy’,optimizer=optimizers.RMSprop(),
                          metrics=[’accuracy’])
    model.summary()
    return model

The makeCuDNNLSTM function constructs and compiles a GPU-optimized LSTM neural network architecture specifically designed for next-day stock price movement prediction, offering significantly faster training and inference compared to the standard LSTM implementation. This function creates a deep learning model that takes as input a sequence of 240 historical daily close-to-close returns and outputs binary classification probabilities predicting whether a stock will outperform or underperform the median on the next trading day. The architecture begins with an Input layer expecting shape (sequence_length, 1) where sequence_length equals 240 representing approximately one trading year of historical daily returns, providing the LSTM with sufficient temporal context to learn patterns in stock price momentum, mean reversion, and other time-series characteristics. This input is fed into a CuDNNLSTM layer with a configurable number of memory cells (default 25), which is a highly optimized implementation of LSTM that leverages CUDA operations for GPU acceleration, running significantly faster than standard LSTM by using fused operations and optimized memory access patterns, though it requires a compatible NVIDIA GPU to function. The return_sequences parameter is set to False because we only need the final hidden state after processing all 240 timesteps rather than outputs at each timestep, as we’re making a single prediction about the next day’s performance rather than a sequence-to-sequence prediction. Following the CuDNNLSTM layer, a Dropout layer with rate 0.1 randomly sets 10 percent of the LSTM outputs to zero during training, providing regularization to prevent overfitting by forcing the network to learn robust features that don’t depend on any single neuron. The final Dense layer with 2 neurons and softmax activation converts the LSTM’s learned representation into probability distributions over two classes (bottom 50 percent and top 50 percent performers for the next day), where the two output values sum to 1.0 and each represents the predicted probability of belonging to that class. The model is compiled with categorical cross-entropy loss which is the standard loss function for multi-class classification and measures how well the predicted probabilities match the true one-hot encoded labels, and the RMSprop optimizer is used because it adapts learning rates based on recent gradients, working particularly well with recurrent neural networks that can suffer from vanishing or exploding gradients. The model summary is printed to display architecture details including layer types, output shapes, and the number of trainable parameters, and finally the compiled model is returned to be used in the trainer function for fitting on historical return data and generating next-day performance predictions.

def callbacks_req(model_type=’LSTM’):
    csv_logger = CSVLogger(model_folder+’/training-log-’+model_type+’-’+str(test_year)+’.csv’)
    filepath = model_folder+”/model-” + model_type + ‘-’ + str(test_year) + “-E{epoch:02d}.h5”
    model_checkpoint = ModelCheckpoint(filepath, monitor=’val_loss’,save_best_only=True)
    earlyStopping = EarlyStopping(monitor=’val_loss’,mode=’min’,patience=10,restore_best_weights=True)
    return [csv_logger,earlyStopping,model_checkpoint]

The callbacks_req function creates and returns a list of Keras callback objects that monitor and control the training process of the LSTM neural network for next-day prediction, providing functionality for logging training metrics, saving model checkpoints, and implementing early stopping to prevent overfitting. This function sets up three essential callbacks that work together throughout the training process: CSVLogger records all training metrics (training loss, validation loss, training accuracy, validation accuracy) to a CSV file after each epoch, creating a permanent record in the model folder with a filename that includes the model type and test year, allowing researchers to analyze training dynamics, diagnose convergence issues, and compare performance across different years and model configurations. ModelCheckpoint automatically saves the model architecture and weights to an HDF5 file, but unlike the intraday models, this version has save_best_only set to True, meaning it only saves the model when the validation loss improves rather than after every epoch, which conserves disk space and ensures we keep only the best-performing model rather than a complete training history. The filepath includes the model type, test year, and epoch number formatted as two digits, and when save_best_only is True, the saved file will be overwritten each time a better model is found, so the final saved model represents the epoch with the lowest validation loss. EarlyStopping is the most critical callback for preventing overfitting, as it monitors the validation loss and stops training if this metric fails to improve for 10 consecutive epochs (patience=10), and when it does stop, it automatically restores the model weights from the epoch that had the best validation loss (restore_best_weights=True), ensuring that the final model is the one that generalizes best to unseen data rather than one that has overfit by training too long. These three callbacks are returned as a list that can be directly passed to the callbacks parameter of the model.fit method, and they work together seamlessly during training: the CSV logger provides transparency and permanent records of the training process, the model checkpoint preserves only the best model to save disk space, and early stopping ensures optimal generalization by preventing the model from memorizing training patterns, which is especially important for next-day prediction where overfitting to historical patterns can lead to poor performance on future data.

def trainer(train_data,test_data,model_type=’CuDNNLSTM’):
    np.random.shuffle(train_data)
    train_x,train_y = train_data[:,2:-2],train_data[:,-1]
    train_x = np.reshape(train_x,(len(train_x),sequence_length,1))
    train_y = np.reshape(train_y,(-1, 1))
    
    enc = OneHotEncoder(handle_unknown=’ignore’)
    enc.fit(train_y)
    enc_y = enc.transform(train_y).toarray()

    if model_type == ‘LSTM’:
        model = makeSimpleLSTM()
    elif model_type == ‘CuDNNLSTM’:
        model = makeCuDNNLSTM()
    else:
        return
    callbacks = callbacks_req(model_type)
    
    model.fit(train_x,
              enc_y,
              epochs=1000,
              validation_split=0.2,
              callbacks=callbacks,
              batch_size=512
              )

    dates = list(set(test_data[:,0]))
    predictions = {}
    for day in dates:
        test_d = test_data[test_data[:,0]==day]
        test_d = np.reshape(test_d[:,2:-2],(len(test_d),sequence_length,1))
        predictions[day] = model.predict(test_d)[:,1]
    return predictions

The trainer function orchestrates the complete training process for the LSTM neural network for next-day stock price prediction, including data preparation, model creation, training with early stopping, and generating predictions on the test set. This function serves as the central machine learning pipeline for the next-day trading strategy, differing from the intraday version primarily in that it predicts next-day close-to-close returns rather than same-day intraday returns. The function begins by shuffling the training data using np.random.shuffle to randomize the order of stock-day observations, which is crucial for neural network training because it prevents the model from learning spurious patterns based on data ordering and ensures that each mini-batch during training contains a diverse mix of examples from different stocks and time periods. After shuffling, the function extracts two components from the training data: train_x contains all feature columns (columns 2 through second-to-last) which are the 240 historical daily return features, and train_y contains the last column which is the binary label (0 or 1) indicating whether the stock was in the bottom or top 50 percent of performers on the next day. The train_x features are reshaped from a 2D array into a 3D array with shape (num_samples, sequence_length, 1) because LSTM layers require 3D input where the dimensions represent samples, timesteps, and features, and in this case we have sequence_length (240) timesteps and 1 feature (daily return) per timestep. The labels train_y are reshaped into a column vector and then transformed using OneHotEncoder, which converts the binary labels (0 or 1) into two-column one-hot encoded format where class 0 becomes [1, 0] and class 1 becomes [0, 1], which is required for categorical cross-entropy loss and allows the model to output separate probabilities for each class. The function then checks the model_type parameter and calls either makeSimpleLSTM for the standard CPU-compatible LSTM or makeCuDNNLSTM for the GPU-optimized version, providing flexibility to run on different hardware configurations, and it also calls callbacks_req to get the list of training callbacks for logging, checkpointing, and early stopping. The core training happens in the model.fit call, which trains the network for up to 1000 epochs (though early stopping will likely halt training much sooner when validation loss stops improving), uses 20 percent of the training data for validation to monitor overfitting, processes data in batches of 512 samples for efficient GPU computation, and applies the callbacks to monitor and control the training process. After training completes, the function generates predictions on the test set by first extracting all unique dates from the test data, then for each date selecting all stocks trading on that day, reshaping their features into the required 3D format (num_stocks, sequence_length, 1), and using model.predict to get probability predictions, specifically extracting the second column ([:,1]) which represents the probability of being in the top 50 percent class for next-day performance. These predictions are stored in a dictionary with dates as keys and arrays of probabilities as values, and finally the function returns this predictions dictionary which will be used by the simulate function to construct long-short portfolios by buying stocks with high predicted probabilities of outperforming and shorting stocks with low predicted probabilities.

def trained(filename,train_data,test_data):
    model = load_model(filename)
    dates = list(set(test_data[:,0]))
    predictions = {}
    for day in dates:
        test_d = test_data[test_data[:,0]==day]
        test_d = np.reshape(test_d[:,2:-2],(len(test_d),sequence_length,1))
        predictions[day] = model.predict(test_d)[:,1] 
    return predictions

The trained function loads a previously saved LSTM model from disk and uses it to generate predictions on test data without retraining, providing functionality for model deployment, result reproduction, and analysis of saved models without the computational cost of retraining. This function is particularly valuable for next-day prediction models because training can take considerable time, and being able to load and reuse trained models saves computational resources and allows for consistent reproduction of published results. The function takes three parameters: filename is the path to a saved Keras model file in HDF5 format (typically with .h5 extension) that was created during a previous training run by the ModelCheckpoint callback, train_data is included in the function signature but is not actually used in the current implementation (possibly for future enhancements or API consistency with other functions), and test_data contains the test set observations with features and labels. The function begins by calling load_model from Keras which reads the HDF5 file and reconstructs the complete model including its architecture (the Input, LSTM or CuDNNLSTM, Dropout, and Dense layers), all trained weights and biases, the optimizer state, and compilation settings, essentially restoring the exact model that was saved during training. After loading the model, the function generates predictions using the same process as the trainer function: it extracts all unique dates from the test data, then for each date selects all stocks trading on that day, extracts their feature columns (columns 2 through second-to-last which are the 240 historical daily return features), reshapes them into the 3D format required by LSTM (num_stocks, sequence_length, 1), and calls model.predict to get probability predictions for each stock. The predictions are stored in a dictionary with dates as keys and the second column of the prediction output ([:,1]) as values, where this second column represents the predicted probability that each stock will be in the top 50 percent of next-day performers. Finally, the function returns this predictions dictionary, allowing the calling code to use these predictions for backtesting the trading strategy and evaluating performance. While this function is defined in the script, it’s not called in the main execution loop which always trains new models, but it provides valuable functionality for researchers who want to analyze previously trained next-day prediction models, reproduce published results without retraining, or deploy models in production environments where real-time predictions are needed without the overhead of training.

def simulate(test_data,predictions):
    rets = pd.DataFrame([],columns=[’Long’,’Short’])
    k = 10
    for day in sorted(predictions.keys()):
        preds = predictions[day]
        test_returns = test_data[test_data[:,0]==day][:,-2]
        top_preds = predictions[day].argsort()[-k:][::-1] 
        trans_long = test_returns[top_preds]
        worst_preds = predictions[day].argsort()[:k][::-1] 
        trans_short = -test_returns[worst_preds]
        rets.loc[day] = [np.mean(trans_long),np.mean(trans_short)] 
        
    return rets

The simulate function implements the actual next-day trading strategy by converting the LSTM model’s probability predictions into concrete portfolio positions and calculating the resulting returns through a long-short equity strategy. This function differs from the intraday version in that it trades based on predictions of next-day close-to-close returns rather than same-day intraday returns, meaning positions are held overnight and the strategy captures multi-day price movements. The function takes two inputs: test_data is the numpy array containing all test set observations including dates, stock names, the 240 historical return features, actual future returns that will be realized, and labels, and predictions is a dictionary mapping each date to an array of predicted probabilities for all stocks trading on that date. The function initializes an empty pandas DataFrame called rets with two columns named ‘Long’ and ‘Short’ to separately track returns from long positions (buying stocks predicted to outperform) and short positions (selling stocks predicted to underperform), and sets k equal to 10 which defines the portfolio size as the top 10 stocks for each leg of the strategy. The main simulation loop iterates through all dates in sorted chronological order to ensure the backtest processes days sequentially as they would occur in real trading, maintaining temporal integrity and preventing look-ahead bias, and for each day it retrieves the prediction probabilities for all stocks and the actual realized next-day returns from the test_data array (column -2 contains the future returns that were actually achieved from today’s close to tomorrow’s close). To construct the long portfolio, the function uses argsort on the predictions array which returns indices that would sort the array in ascending order, takes the last k indices using [-k:] which correspond to the k highest probability predictions (stocks the LSTM believes are most likely to be top performers tomorrow), reverses them with [::-1] to get descending order, and uses these indices to select the actual returns of the top 10 predicted stocks from test_returns, storing them in trans_long. Similarly, for the short portfolio, it takes the first k indices from argsort using [:k] which correspond to the k lowest probability predictions (stocks predicted to be worst performers tomorrow), reverses them, and selects their actual returns, multiplying by negative one using -test_returns because in short selling you profit when the stock price declines, so a negative return (stock went down) becomes a positive profit for the short position. The function then calculates the mean return of the 10 long positions and the mean return of the 10 short positions, storing both values in the rets DataFrame for that day using rets.loc[day], effectively creating an equal-weighted portfolio within each leg where each of the 10 stocks contributes equally to that leg’s performance. After processing all trading days in the test period, the function returns the rets DataFrame containing the complete time series of daily long and short returns, which the calling code will then sum together (long plus short returns) to get total daily strategy returns and pass to the Statistics class for comprehensive performance analysis including calculation of mean returns, Sharpe ratio, maximum drawdown, and other risk-adjusted metrics that quantify how well the LSTM-based next-day trading strategy performed.

def create_label(df,perc=[0.5,0.5]):
    perc = [0.]+list(np.cumsum(perc))
    label = df.iloc[:,1:].pct_change(fill_method=None)[1:].apply(
        lambda x: pd.qcut(x.rank(method=’first’),perc,labels=False), axis=1)
    return label

The create_label function generates binary classification labels for all stocks on each trading day by calculating their next-day close-to-close returns and ranking them to identify top and bottom performers, creating the supervised learning targets that the LSTM model will learn to predict. This function differs from the intraday version in that it labels stocks based on their next-day performance (today’s close to tomorrow’s close) rather than intraday performance (today’s open to today’s close), making it suitable for next-day prediction strategies. The function takes two parameters: df is a DataFrame containing closing prices with dates in the first column and stock ticker symbols as column headers for subsequent columns, and perc is a list defining the percentile boundaries for classification with a default of [0.5, 0.5] which creates a binary split at the median (50th percentile). The function first transforms the perc list by prepending 0 and computing the cumulative sum, so [0.5, 0.5] becomes [0.0, 0.5, 1.0], which defines the quantile boundaries where 0.0 to 0.5 represents the bottom 50 percent of stocks and 0.5 to 1.0 represents the top 50 percent. The core labeling logic calculates next-day returns by first excluding the date column (iloc[:,1:]), then computing percentage changes using pct_change with fill_method set to None to avoid forward-filling missing values, which gives the daily close-to-close return for each stock, and then taking [1:] to exclude the first row which cannot have a percentage change since there’s no previous day. The function then applies a lambda function row-wise (axis=1) that processes each day independently, first ranking all stocks on that day by their next-day returns using rank with method=’first’ to handle ties by assigning ranks based on order of appearance, then using pd.qcut to bin these ranks into quantiles based on the perc boundaries, assigning label 0 to stocks in the bottom 50 percent and label 1 to stocks in the top 50 percent. The qcut function with labels=False returns integer labels (0, 1) rather than interval labels, creating a clean binary classification target. The function returns this label DataFrame which contains 0s and 1s indicating whether each stock was a bottom or top performer on the next day, and these labels are used throughout the training process as the target variable that the LSTM learns to predict based on historical daily return patterns, and during backtesting the labels help evaluate prediction accuracy and assess how well the model identifies future winners and losers for next-day trading.

def create_stock_data(df,st):
    daily_change = df[st].pct_change()
    st_data = pd.DataFrame([])
    st_data[’Date’] = list(df[’Date’])
    st_data[’Name’] = [st]*len(st_data)
    for k in range(240)[::-1]:
        st_data[’R’+str(k)] = daily_change.shift(k)
    st_data[’R-future’] = daily_change.shift(-1)    
    st_data[’label’] = list(label[st])+[np.nan] 
    st_data[’Month’] = list(df[’Date’].str[:-3])
    st_data = st_data.dropna()
    
    trade_year = st_data[’Month’].str[:4]
    st_data = st_data.drop(columns=[’Month’])
    st_train_data = st_data[trade_year<str(test_year)]
    st_test_data = st_data[trade_year==str(test_year)]
    return np.array(st_train_data),np.array(st_test_data)

The create_stock_data function constructs the complete feature set and labels for a single stock by calculating historical daily close-to-close returns and organizing them into a format suitable for LSTM training and prediction for next-day performance forecasting. This function creates a time series dataset where each row represents a trading day with 240 features representing past daily returns, providing the LSTM with sufficient historical context to learn temporal patterns that might predict next-day performance. The function takes two parameters: df is a DataFrame containing closing prices for all stocks across all dates with dates in the first column and stock tickers as subsequent column headers, and st is the ticker symbol of the specific stock being processed. The function begins by calculating daily_change as the daily percentage change in closing prices using pct_change, which gives the close-to-close return representing the percentage change from one day’s close to the next day’s close, capturing the overall daily price movement that includes both intraday changes and overnight gaps. The function then creates an empty DataFrame and populates it with a Date column copied from the input DataFrame and a Name column filled with the stock ticker repeated for every row, establishing the basic structure. The core feature engineering creates 240 feature columns using a loop that iterates through range(240) in reverse order ([::-1]), and for each value k it creates a column named ‘R’ plus k (like R0, R1, up to R239) by shifting the daily_change series by k positions, where shift(0) gives today’s daily return, shift(1) gives yesterday’s daily return, shift(2) gives the return from two days ago, and so on up to shift(239) giving the return from 239 days ago. This creates a sliding window of historical daily returns where each row contains the current day’s date along with the daily returns from the past 240 days, providing the LSTM with a complete sequence of historical performance to learn temporal patterns from. The function also creates an ‘R-future’ column by shifting daily_change by -1, which gives the next day’s close-to-close return that we’re trying to predict, serving as the actual realized return for backtesting purposes. The label column is added by taking the pre-calculated labels for this stock from the global label variable and appending a NaN value to handle the length mismatch from shifting operations. A Month column is extracted from the date strings to facilitate train-test splitting by year, and then dropna is called to remove any rows with missing values that result from the shifting operations (the first 240 rows won’t have complete history and the last row won’t have a future return). The function then extracts the year from the Month column and uses it to split the data into training and test sets, where training data includes all years before the test_year and test data includes only the test_year, ensuring proper temporal separation that prevents look-ahead bias. Finally, both datasets are converted to numpy arrays and returned as a tuple, providing the calling code with properly formatted training and test data for this stock that can be concatenated with data from other stocks to create the complete dataset for LSTM training and next-day prediction evaluation.

def Normalize(train_data,test_data,norm_type=’StandardScalar’):
    scaler = StandardScaler() if norm_type==’StandardScalar’ else RobustScaler()
    scaler.fit(train_data[:,2:-2])
    train_data[:,2:-2] = scaler.transform(train_data[:,2:-2])
    test_data[:,2:-2] = scaler.transform(test_data[:,2:-2])

model_folder = ‘models-NextDay-240-1-LSTM’
result_folder = ‘results-NextDay-240-1-LSTM’
for directory in [model_folder,result_folder]:
    if not os.path.exists(directory):
        os.makedirs(directory)

model_type = ‘CuDNNLSTM’
norm_type = ‘StandardScalar’

for test_year in range(1993,2020):
    
    print(’-’*40)
    print(test_year)
    print(’-’*40)
    
    filename = ‘data/Close-’+str(test_year-3)+’.csv’
    df = pd.read_csv(filename)
    
    label = create_label(df)
    stock_names = list(constituents[str(test_year-1)+’-12’])
    train_data,test_data = [],[]
    
    start = time.time()
    for st in stock_names:
        st_train_data,st_test_data = create_stock_data(df,st)
        train_data.append(st_train_data)
        test_data.append(st_test_data)

    train_data = np.concatenate([x for x in train_data])
    test_data = np.concatenate([x for x in test_data])
    
    print(’Created :’,train_data.shape,test_data.shape,time.time()-start)
    
    sequence_length = 240
    Normalize(train_data,test_data,norm_type)
    
    predictions = trainer(train_data,test_data,model_type)
    returns = simulate(test_data,predictions)
    result = Statistics(returns.sum(axis=1))
    print(’\nAverage returns prior to transaction charges’)
    result.shortreport() 
    
    with open(result_folder+’/predictions-’+str(test_year)+’.pickle’, ‘wb’) as handle:
        pickle.dump(predictions, handle, protocol=pickle.HIGHEST_PROTOCOL)
    
    returns.to_csv(result_folder+’/avg_daily_rets-’+str(test_year)+’.csv’)
    with open(result_folder+”/avg_returns.txt”, “a”) as myfile:
        res = ‘-’*30 + ‘\n’ 
        res += str(test_year) + ‘\n’
        res += ‘Mean = ‘ + str(result.mean()) + ‘\n’
        res += ‘Sharpe = ‘+str(result.sharpe()) + ‘\n’
        res += ‘-’*30 + ‘\n’
        myfile.write(res)

The Normalize function standardizes the feature values in both training and test datasets to have consistent scales, which is crucial for LSTM training because it helps the optimization algorithm converge faster and prevents features with larger numerical ranges from dominating the learning process. This function provides flexibility by supporting two different normalization methods: StandardScaler which standardizes features by removing the mean and scaling to unit variance, and RobustScaler which uses the median and interquartile range making it more resistant to outliers. The function takes three parameters: train_data and test_data are numpy arrays containing the complete datasets with dates, stock names, the 240 daily return features, future returns, and labels as columns, and norm_type is a string specifying which scaler to use with default ‘StandardScalar’ (note the typo in the parameter name which should be ‘StandardScaler’). The function creates the appropriate scaler object using a conditional expression, instantiating StandardScaler if norm_type equals ‘StandardScalar’ or RobustScaler otherwise, providing flexibility to experiment with different normalization approaches. The normalization process follows the critical machine learning principle of fitting the scaler only on training data to prevent data leakage, so the function calls scaler.fit on train_data[:,2:-2] which selects only the 240 feature columns (skipping the first two columns for Date and Name, and the last two columns for future returns and labels), and this fit operation calculates the normalization parameters (mean and standard deviation for StandardScaler, or median and interquartile range for RobustScaler) based solely on the training set, ensuring that no information from the test set influences the scaling. After fitting, the function transforms both training and test data using these same scaling parameters by calling scaler.transform on the feature columns of both datasets, which applies the normalization (subtracting mean and dividing by standard deviation for StandardScaler, or subtracting median and dividing by interquartile range for RobustScaler), bringing all 240 features to similar scales typically centered around zero. The transformation is applied in-place by assigning the results back to the same column slices ([:,2:-2]), modifying the original arrays, which is memory efficient but means the calling code should be aware that the input arrays are modified. This normalization is essential for LSTM training because it ensures that all 240 input features contribute roughly equally to the initial gradients during backpropagation, prevents numerical instability from very large or small values, and helps the network learn faster by keeping activations in ranges where activation functions like tanh have useful gradients, ultimately leading to better model performance and more reliable next-day predictions.

Train NEXT Day Reinforcement Learning

def trainer(train_data,test_data):
    random.seed(SEED)
    np.random.seed(SEED)
    
    train_x,train_y = train_data[:,2:-2],train_data[:,-1]
    train_y = train_y.astype(’int’)

    print(’Started training’)
    clf = RandomForestClassifier(n_estimators=1000, max_depth=20, random_state = SEED, n_jobs=-1)
    clf.fit(train_x,train_y)
    print(’Completed ‘,clf.score(train_x,train_y))

    dates = list(set(test_data[:,0]))
    predictions = {}
    for day in dates:
        test_d = test_data[test_data[:,0]==day]
        test_d = test_d[:,2:-2] 
        predictions[day] = clf.predict_proba(test_d)[:,1]
    return predictions

The trainer function implements the complete training and prediction pipeline for the Random Forest classifier for next-day stock price movement prediction, learning to identify stocks that will outperform or underperform on the next trading day by analyzing patterns in historical multi-period return features. This function represents the Random Forest approach to next-day prediction, offering an alternative to LSTM that treats each stock-day observation as an independent sample with engineered features rather than modeling temporal sequences. The function begins by resetting random seeds for both Python’s random module and numpy to ensure reproducibility, which is critical for Random Forest because the algorithm involves random sampling when building each tree through bootstrap aggregating (randomly sampling data with replacement) and random feature selection at each split point, and fixing these seeds ensures that the same trees are built across different runs with the same data. After setting seeds, the function extracts features and labels from the training data by slicing the numpy array: train_x contains columns 2 through second-to-last which are the multi-period return features calculated at various lookback periods (1 to 20 days, then 40 to 240 days in 20-day increments), and train_y contains the last column which is the binary label (0 or 1) indicating whether the stock was in the bottom or top 50 percent of next-day performers. The labels are explicitly cast to integer type using astype(‘int’) to ensure compatibility with the Random Forest classifier which expects integer class labels for classification tasks. The function then prints a status message and creates a RandomForestClassifier object with carefully chosen hyperparameters: n_estimators equals 1000 meaning the forest will contain 1000 individual decision trees that vote together to make predictions, max_depth equals 20 which is notably larger than the 10 used in intraday models, allowing trees to grow deeper and capture more complex patterns in next-day prediction which may require learning more intricate decision boundaries, random_state is set to SEED for reproducibility of the random processes within the forest, and n_jobs equals -1 which tells scikit-learn to use all available CPU cores for parallel training of the trees, significantly speeding up the training process. The clf.fit call trains the Random Forest on the training data, where each of the 1000 trees is built by randomly sampling the data with replacement (bootstrap sampling) and randomly selecting a subset of features at each split point, creating diversity among the trees that helps the ensemble generalize better than any single tree. After training completes, the function prints the training accuracy using clf.score, which shows what percentage of training samples were correctly classified, though this is primarily for monitoring purposes and high training accuracy doesn’t necessarily indicate good generalization to unseen data. The function then generates predictions on the test set by first extracting all unique dates from the test data, then for each date selecting all stocks trading that day, extracting their features (columns 2 through second-to-last), and calling clf.predict_proba to get probability predictions rather than hard class assignments. The predict_proba method returns a 2D array where each row corresponds to a stock and contains two probabilities summing to 1.0, with the first column representing the probability of class 0 (bottom 50 percent) and the second column ([:,1]) representing the probability of class 1 (top 50 percent), and we extract this second column because we want to rank stocks by their predicted likelihood of being top performers on the next day. These probabilities are stored in a dictionary with dates as keys and arrays of probabilities as values, and finally the function returns this predictions dictionary which will be used by the simulate function to construct long-short portfolios by buying stocks with high predicted probabilities of outperforming tomorrow and shorting stocks with low predicted probabilities.

def simulate(test_data,predictions):
    rets = pd.DataFrame([],columns=[’Long’,’Short’])
    k = 10
    for day in sorted(predictions.keys()):
        preds = predictions[day]
        test_returns = test_data[test_data[:,0]==day][:,-2]
        top_preds = predictions[day].argsort()[-k:][::-1] 
        trans_long = test_returns[top_preds]
        worst_preds = predictions[day].argsort()[:k][::-1] 
        trans_short = -test_returns[worst_preds]
        rets.loc[day] = [np.mean(trans_long),np.mean(trans_short)] 
    return rets

The simulate function implements the actual next-day trading strategy by converting the Random Forest model’s probability predictions into concrete portfolio positions and calculating the resulting returns through a long-short equity strategy. This function is identical to the simulate function in the next-day LSTM model, demonstrating that the same trading logic applies regardless of whether predictions come from a tree-based ensemble or a neural network. The function takes two inputs: test_data is the numpy array containing all test set observations including dates, stock names, features, actual future returns that will be realized, and labels, and predictions is a dictionary mapping each date to an array of predicted probabilities for all stocks trading on that date. The function initializes an empty pandas DataFrame called rets with two columns named ‘Long’ and ‘Short’ to separately track returns from long positions (buying stocks predicted to outperform tomorrow) and short positions (selling stocks predicted to underperform tomorrow), and sets k equal to 10 which defines the portfolio size as the top 10 stocks for each leg of the strategy. The main simulation loop iterates through all dates in sorted chronological order to ensure the backtest processes days sequentially as they would occur in real trading, maintaining temporal integrity and preventing look-ahead bias, and for each day it retrieves the prediction probabilities for all stocks and the actual realized next-day returns from the test_data array (column -2 contains the future returns that were actually achieved from today’s close to tomorrow’s close). To construct the long portfolio, the function uses argsort on the predictions array which returns indices that would sort the array in ascending order, takes the last k indices using [-k:] which correspond to the k highest probability predictions (stocks the Random Forest believes are most likely to be top performers tomorrow based on their multi-period return patterns), reverses them with [::-1] to get descending order, and uses these indices to select the actual returns of the top 10 predicted stocks from test_returns, storing them in trans_long. Similarly, for the short portfolio, it takes the first k indices from argsort using [:k] which correspond to the k lowest probability predictions (stocks predicted to be worst performers tomorrow), reverses them, and selects their actual returns, multiplying by negative one using -test_returns because in short selling you profit when the stock price declines, so a negative return (stock went down) becomes a positive profit for the short position. The function then calculates the mean return of the 10 long positions and the mean return of the 10 short positions, storing both values in the rets DataFrame for that day using rets.loc[day], effectively creating an equal-weighted portfolio within each leg where each of the 10 stocks contributes equally to that leg’s performance. After processing all trading days in the test period, the function returns the rets DataFrame containing the complete time series of daily long and short returns, which the calling code will then sum together (long plus short returns) to get total daily strategy returns and pass to the Statistics class for comprehensive performance analysis including calculation of mean returns, Sharpe ratio, maximum drawdown, and other risk-adjusted metrics that quantify how well the Random Forest-based next-day trading strategy performed.

def create_label(df,perc=[0.5,0.5]):
    perc = [0.]+list(np.cumsum(perc))
    label = df.iloc[:,1:].pct_change(fill_method=None)[1:].apply(
        lambda x: pd.qcut(x.rank(method=’first’),perc,labels=False), axis=1)
    return label

The create_label function generates binary classification labels for all stocks on each trading day by calculating their next-day close-to-close returns and ranking them to identify top and bottom performers, creating the supervised learning targets that the Random Forest model will learn to predict. This function is identical to the label creation in the next-day LSTM model, demonstrating that the labeling logic remains consistent across different machine learning approaches for the same prediction task. The function takes two parameters: df is a DataFrame containing closing prices with dates in the first column and stock ticker symbols as column headers for subsequent columns, and perc is a list defining the percentile boundaries for classification with a default of [0.5, 0.5] which creates a binary split at the median (50th percentile). The function first transforms the perc list by prepending 0 and computing the cumulative sum, so [0.5, 0.5] becomes [0.0, 0.5, 1.0], which defines the quantile boundaries where 0.0 to 0.5 represents the bottom 50 percent of stocks and 0.5 to 1.0 represents the top 50 percent. The core labeling logic calculates next-day returns by first excluding the date column (iloc[:,1:]), then computing percentage changes using pct_change with fill_method set to None to avoid forward-filling missing values, which gives the daily close-to-close return for each stock representing the percentage change from one day’s close to the next day’s close, and then taking [1:] to exclude the first row which cannot have a percentage change since there’s no previous day. The function then applies a lambda function row-wise (axis=1) that processes each day independently, first ranking all stocks on that day by their next-day returns using rank with method=’first’ to handle ties by assigning ranks based on order of appearance, then using pd.qcut to bin these ranks into quantiles based on the perc boundaries, assigning label 0 to stocks in the bottom 50 percent and label 1 to stocks in the top 50 percent. The qcut function with labels=False returns integer labels (0, 1) rather than interval labels, creating a clean binary classification target. The function returns this label DataFrame which contains 0s and 1s indicating whether each stock was a bottom or top performer on the next day, and these labels are used throughout the training process as the target variable that the Random Forest learns to predict based on historical multi-period return patterns, and during backtesting the labels help evaluate prediction accuracy and assess how well the model identifies future winners and losers for next-day trading.

def create_stock_data(df,st):
    st_data = pd.DataFrame([])
    st_data[’Date’] = list(df[’Date’])
    st_data[’Name’] = [st]*len(st_data)
    for k in list(range(1,21))+list(range(40,241,20)):
        st_data[’R’+str(k)] = df[st].pct_change(k)
    st_data[’R-future’] = df[st].pct_change().shift(-1)    
    st_data[’label’] = list(label[st])+[np.nan] 
    st_data[’Month’] = list(df[’Date’].str[:-3])
    st_data = st_data.dropna()
    
    trade_year = st_data[’Month’].str[:4]
    st_data = st_data.drop(columns=[’Month’])
    st_train_data = st_data[trade_year<str(test_year)]
    st_test_data = st_data[trade_year==str(test_year)]
    return np.array(st_train_data),np.array(st_test_data)

result_folder = ‘results-NextDay-240-1-RF’
for directory in [result_folder]:
    if not os.path.exists(directory):
        os.makedirs(directory)

for test_year in range(1993,2020):
    
    print(’-’*40)
    print(test_year)
    print(’-’*40)
    
    filename = ‘data/Close-’+str(test_year-3)+’.csv’
    df = pd.read_csv(filename)
    
    label = create_label(df)
    stock_names = sorted(list(constituents[str(test_year-1)+’-12’]))
    train_data,test_data = [],[]
    
    start = time.time()
    for st in stock_names:
        st_train_data,st_test_data = create_stock_data(df,st)
        train_data.append(st_train_data)
        test_data.append(st_test_data)

    train_data = np.concatenate([x for x in train_data])
    test_data = np.concatenate([x for x in test_data])
    
    print(’Created :’,train_data.shape,test_data.shape,time.time()-start)
    
    
    predictions = trainer(train_data,test_data)
    returns = simulate(test_data,predictions)
    result = Statistics(returns.sum(axis=1))
    print(’\nAverage returns prior to transaction charges’)
    result.shortreport() 
    
    with open(result_folder+’/predictions-’+str(test_year)+’.pickle’, ‘wb’) as handle:
        pickle.dump(predictions, handle, protocol=pickle.HIGHEST_PROTOCOL)
    
    returns.to_csv(result_folder+’/avg_daily_rets-’+str(test_year)+’.csv’)
    with open(result_folder+”/avg_returns.txt”, “a”) as myfile:
        res = ‘-’*30 + ‘\n’ 
        res += str(test_year) + ‘\n’
        res += ‘Mean = ‘ + str(result.mean()) + ‘\n’
        res += ‘Sharpe = ‘+str(result.sharpe()) + ‘\n’
        res += ‘-’*30 + ‘\n’
        myfile.write(res)

The create_stock_data function constructs the complete feature set and labels for a single stock by calculating multi-period close-to-close returns at various lookback periods, creating a dataset specifically designed for Random Forest models that captures both short-term and long-term price momentum patterns for next-day prediction. This function differs from the LSTM version in its feature engineering approach: instead of creating 240 consecutive daily returns as a time series for LSTM, it creates a smaller set of strategically chosen multi-period returns that capture key momentum signals at different time scales, which is more suitable for Random Forest models that treat features independently rather than as sequences. The function takes two parameters: df is a DataFrame containing closing prices for all stocks across all dates with dates in the first column and stock tickers as subsequent column headers, and st is the ticker symbol of the specific stock being processed. The function begins by creating an empty DataFrame and populating it with a Date column copied from the input DataFrame and a Name column filled with the stock ticker repeated for every row, establishing the basic structure. The core feature engineering uses a carefully designed set of lookback periods defined by list(range(1,21)) plus list(range(40,241,20)), which creates the list [1, 2, 3, …, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240], providing dense coverage of recent history (daily granularity for the past 20 days) and sparser coverage of more distant history (every 20 days from 40 to 240 days ago), totaling approximately 32 features. For each lookback period k in this list, the function creates a feature column named ‘R’ plus k by calculating df[st].pct_change(k), which computes the k-period percentage change in closing prices, representing the cumulative return over the past k days. For example, pct_change(1) gives the 1-day return (yesterday to today), pct_change(5) gives the 5-day return (5 days ago to today), and pct_change(240) gives the 240-day return (approximately one year ago to today). These multi-period returns capture momentum at different time scales: short-period returns (1–20 days) capture recent momentum and potential mean reversion, while longer-period returns (40–240 days) capture longer-term trends and momentum persistence. The function creates an ‘R-future’ column by calculating df[st].pct_change().shift(-1), which gives the next day’s close-to-close return that we’re trying to predict, serving as the actual realized return for backtesting purposes. The label column is added by taking the pre-calculated labels for this stock from the global label variable and appending a NaN value to handle the length mismatch from shifting operations. A Month column is extracted from the date strings to facilitate train-test splitting by year, and then dropna is called to remove any rows with missing values that result from the pct_change and shift operations (the first 240 rows won’t have complete history for the longest lookback period, and the last row won’t have a future return). The function then extracts the year from the Month column and uses it to split the data into training and test sets, where training data includes all years before the test_year and test data includes only the test_year, ensuring proper temporal separation that prevents look-ahead bias. Finally, both datasets are converted to numpy arrays and returned as a tuple, providing the calling code with properly formatted training and test data for this stock that can be concatenated with data from other stocks to create the complete dataset for Random Forest training and next-day prediction evaluation.