Advanced State Space Models for Accurate Stock Prediction: Leveraging Mamba and S4 to Capture Complex Market Dynamics
From ARIMA to Mamba: A New Era in Modeling Financial Market Patterns
Predicting stock prices has long been a complex challenge, yet it remains one of the most sought-after goals in finance. Accurate predictions allow investors and financial institutions to make well-informed decisions, manage risks, and maximize returns. The stock market’s volatility and its sensitivity to a wide array of factors, including economic data, global events, and investor sentiment, make precise forecasting both challenging and essential. In today’s data-driven world, the financial sector is constantly searching for advanced tools to improve the accuracy of stock predictions, with profound implications for economic growth and individual wealth.
The importance of stock markets to global economic health cannot be overstated. Stock exchanges worldwide represent a measure of economic strength and investor confidence, reflecting how businesses are expected to perform over time. Investors, including individuals, corporations, and governments, actively monitor and invest in stock markets as a way to grow wealth, fund public projects, or secure financial stability for future generations. A key reason for this interest is the potential for high returns; however, such potential is accompanied by considerable risks. Misjudging market trends can lead to significant financial losses. As such, accurately predicting stock prices is a critical component in minimizing investment risk and stabilizing financial markets.
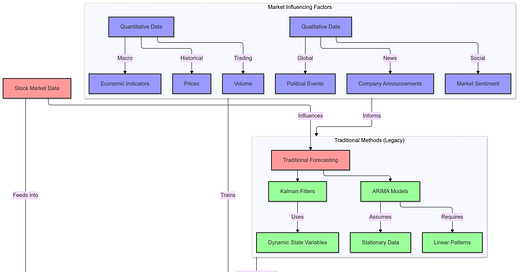
Despite its importance, stock price prediction is exceptionally difficult due to the market’s inherent nonlinearity and unpredictability. Stock prices are influenced by an enormous number of variables, both quantitative (like historical prices, volume, and macroeconomic indicators) and qualitative (such as political events, company announcements, or market sentiment). This combination of diverse and complex factors results in nonlinear patterns, which traditional forecasting models struggle to capture. Traditional time-series models like ARIMA (Auto-Regressive Integrated Moving Average) have been commonly used for stock prediction because they can forecast based on past data trends. However, ARIMA and similar statistical methods operate on assumptions of linearity and stationarity, which are often not met in real-world stock data. This discrepancy between model assumptions and the reality of stock market behavior limits the predictive accuracy of these methods, especially during periods of high volatility or economic upheaval.
The ARIMA model, for instance, relies on the premise that stock prices follow a linear pattern that can be decomposed into past values and error terms. This model is most effective when the underlying data exhibits stationarity, meaning its statistical properties (like mean and variance) do not change over time. However, stock prices often fluctuate unpredictably, influenced by external factors that do not follow a fixed pattern. Additionally, ARIMA requires substantial pre-processing, such as differencing and detrending, to fit the data into a stationary format. Even when these requirements are met, the model’s linear nature means it cannot fully capture the complex, nonlinear relationships in stock data, which can result in inconsistent or inaccurate predictions.
Another traditional tool is the Kalman Filter, which represents stock prices in terms of dynamic state variables. Although Kalman Filters are useful in modeling sequential data, they also rely heavily on assumptions of linearity and Gaussian noise, making them limited in handling the nonlinear volatility typical in stock markets. As financial data has become more accessible and abundant, these traditional models’ shortcomings have become increasingly apparent, prompting a shift toward more advanced forecasting methods.
Enter the realm of artificial intelligence (AI) and deep learning, which has brought about a paradigm shift in stock prediction methodologies. Deep learning models, particularly those designed for sequence and time-series data, can accommodate the complex, nonlinear patterns inherent in stock prices. These models, especially those that integrate structured state spaces, provide a novel approach to capturing sequential dependencies and nonlinear relationships without the strict assumptions of traditional models. Neural networks, recurrent architectures, and transformer-based models have shown promise in predicting stock price movements by adapting to various factors and learning patterns that traditional models overlook.
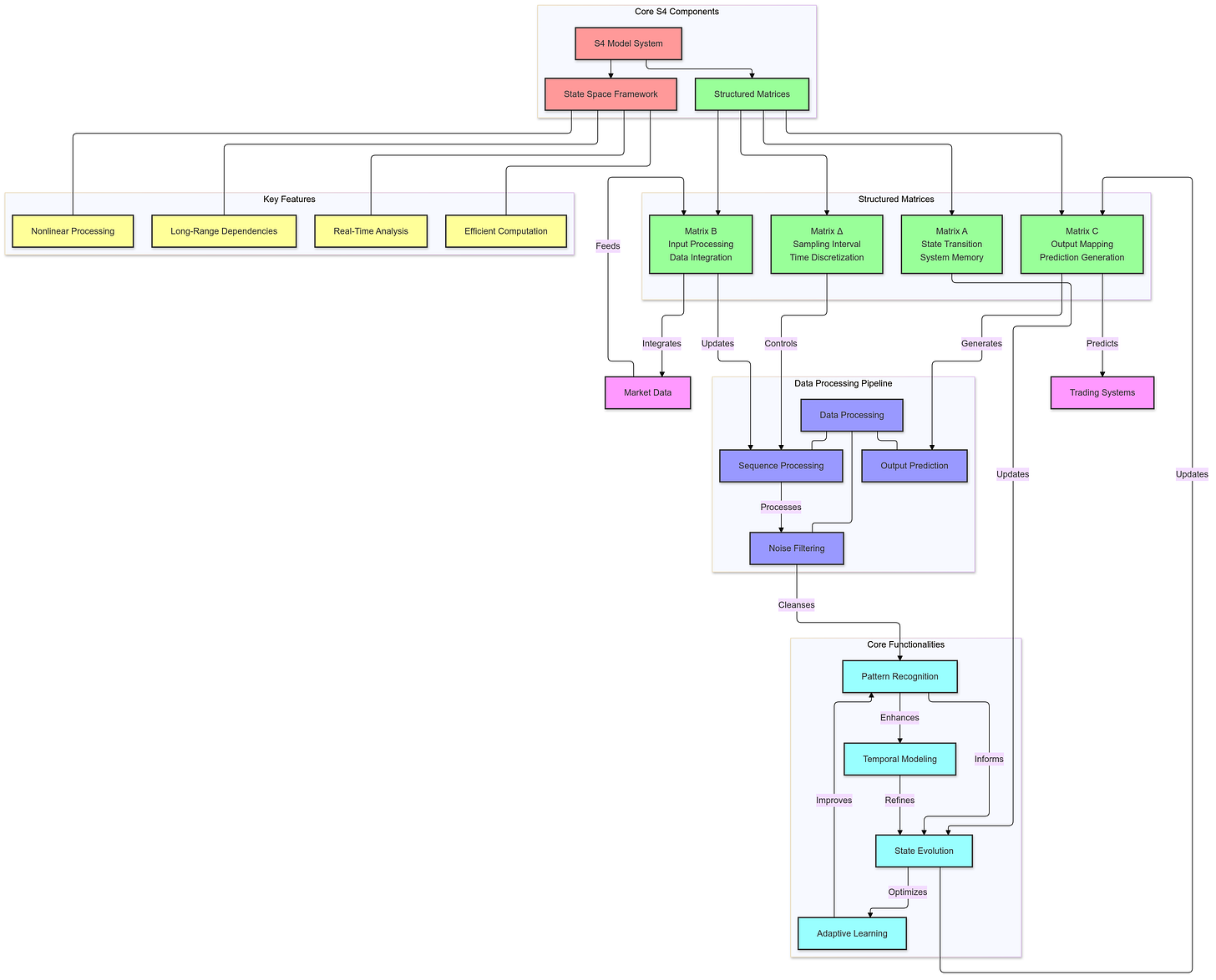
One of the most innovative developments in this space is the use of Structured State Space Models (S4), which leverage a state-space framework traditionally used in control theory to handle sequential data with greater accuracy. The S4 model represents the dynamics of sequential data through structured matrices that capture the evolution of data states over time. Unlike traditional state-space models, which rely on unstructured matrices and thus face limitations in capturing complex dependencies, structured state spaces use specialized matrix representations. This approach provides two main benefits: (1) efficient computation, even over long sequences, which is critical for analyzing large financial datasets; and (2) the ability to retain relevant past information while filtering out noise, ensuring that the model focuses on essential data for accurate predictions.
However, even the S4 model can face challenges in ignoring irrelevant data and maintaining efficiency with very large datasets. The introduction of the Mamba model (S6) addresses these limitations by enhancing S4 with a selection mechanism and scan module. The selection mechanism enables the model to dynamically choose which parts of the input sequence are relevant for prediction, effectively filtering out noisy data. This targeted focus allows the model to capture important dependencies and patterns that significantly influence stock movements. The scan module further enhances the model’s capability by processing the sequence with linear time complexity, which means it can handle large-scale data without compromising speed or efficiency. This setup is particularly advantageous in financial forecasting, where real-time processing of large volumes of data is often required.
These advanced models, equipped with state-space representations and deep learning techniques, are also more robust to shifts in market conditions. While traditional models often falter under unusual market circumstances, such as financial crises or sudden economic shocks, AI-based models can adapt to changes by learning from diverse data sources. In essence, they capture both local dependencies (short-term trends) and global patterns (long-term dependencies), allowing for more accurate and reliable stock price predictions.
In recent years, the addition of more sophisticated components like the hyperbolic tangent (tanh) activation function has further improved AI-based stock prediction models. The tanh function maps input values to an output range between -1 and 1, a bounded interval that is ideal for modeling stock price movement rates, as it prevents the model from predicting unreasonably high or low values. This bounded output is particularly useful for financial applications, where predictions need to stay within realistic limits.
Another critical factor contributing to the improved performance of AI-based models in stock prediction is the use of Mean Squared Error (MSE) as the primary loss function. MSE calculates the average squared difference between predicted and actual values, making it sensitive to large errors. For financial predictions, where large errors can have substantial consequences, minimizing MSE is crucial for enhancing model accuracy. Paired with the Adam optimizer, which dynamically adjusts the learning rate based on gradients, the model is better equipped to converge on an optimal solution during training.
Understanding Traditional Models and Their Limitations
Traditional models have long been employed in time-series forecasting, including in the stock market, due to their simplicity and mathematical foundations. However, as financial markets grow more complex and influenced by diverse, often unpredictable factors, these models struggle to provide accurate predictions. Here, we explore the ARIMA model and Kalman Filters, two foundational time-series models, and explain why they often fall short in the context of volatile, nonlinear stock market data. We also touch on hybrid models like ARIMA-NN, which attempt to bridge the gap by combining traditional methods with modern neural networks but still inherit key limitations.
ARIMA Model
The ARIMA model, short for Auto-Regressive Integrated Moving Average, is a commonly used statistical tool for forecasting time-series data. ARIMA is a linear model that analyzes and predicts data based on the assumption that future values can be estimated by looking at patterns in past data, decomposing time-series data into three components:
Auto-Regressive (AR): This component uses past observations to predict future values. It assumes that there is a relationship between the current value and a certain number of lagged values.
Integrated (I): This step makes the data stationary by differencing it, which means calculating the differences between consecutive data points to remove trends and stabilize the mean of the time series.
Moving Average (MA): This component uses the residuals (errors) from previous predictions to fine-tune the forecast.
Despite its usefulness in certain stationary, linear time series, ARIMA has significant limitations, particularly in the stock market, where the data is rarely stationary or linear. Financial data is affected by a myriad of factors such as investor sentiment, global economic events, and market speculation, leading to high volatility and nonlinearity. ARIMA requires the data to be “stationary,” meaning it assumes that the statistical properties of the series (like the mean and variance) do not change over time. To make financial data stationary, extensive preprocessing is often necessary, including differencing and detrending, which may lose valuable information and make the model less effective.
Another core limitation of ARIMA is its reliance on linear relationships, assuming that future values can be directly predicted by past values in a straightforward, proportional manner. In the financial world, however, price movements are often influenced by nonlinear factors that interact in unpredictable ways. ARIMA’s linear framework cannot effectively capture these relationships, leading to inaccuracies in stock predictions, especially during periods of sudden change, such as market crashes or rallies. In highly dynamic financial environments, the inability to adapt to nonlinear patterns severely limits ARIMA’s effectiveness, making it an unreliable choice for complex stock market forecasting.
Kalman Filters
Kalman Filters, another traditional tool used in time-series analysis, are based on state-space models, a mathematical framework that represents the system being modeled in terms of state variables. Kalman Filters were initially developed to track the position and velocity of objects, such as spacecraft or vehicles, by continually updating estimates based on new observations. In time-series analysis, Kalman Filters are used to track changes over time by modeling a system’s internal state as it evolves. The Kalman Filter essentially predicts the next state based on the current state and then updates this prediction by incorporating new observations, thus continuously refining the prediction as new data arrives.
While effective in domains like signal processing and control systems, where data follows relatively predictable, continuous trends, Kalman Filters face limitations in stock market prediction. One primary reason is that Kalman Filters are inherently linear models, like ARIMA, assuming that changes over time can be represented through a set of linear equations. This assumption is often invalid in financial markets, where nonlinear relationships dominate. Furthermore, Kalman Filters work under the assumption of Gaussian noise, which assumes that the deviations from predicted values follow a normal distribution. In reality, stock market data frequently deviates from this norm, exhibiting heavy tails and skewed distributions during periods of volatility. As a result, Kalman Filters struggle to accurately track stock price movements in the face of sudden, large deviations from historical trends.
Another limitation of Kalman Filters in financial markets is their sensitivity to noise. Stock prices are notoriously volatile, with frequent short-term fluctuations that may not indicate any meaningful trend or pattern. Kalman Filters, which are designed to react quickly to new observations, can often mistake this noise for a significant change, leading to overreactive predictions. This sensitivity to minor fluctuations makes Kalman Filters less reliable in financial forecasting, where the goal is often to identify meaningful trends rather than react to every small price movement.
Hybrid Models: The Case of ARIMA-NN
To address the limitations of traditional linear models, some researchers have proposed hybrid models, combining ARIMA with neural networks. One prominent example is the ARIMA-NN model, which combines the statistical forecasting capabilities of ARIMA with the nonlinear pattern recognition abilities of neural networks. The rationale behind this approach is that ARIMA can capture the linear, predictable components of the data, while a neural network can handle the residuals, identifying any nonlinear patterns left unexplained by ARIMA.
In practice, the ARIMA-NN model works by first using ARIMA to forecast the time series, effectively modeling the linear components. Then, the neural network takes the residuals (the difference between the actual and ARIMA-predicted values) and tries to predict these remaining patterns, theoretically filling in the gaps that ARIMA misses. While this approach represents an improvement over pure ARIMA, it still inherits key limitations from its traditional counterpart. Because ARIMA remains the primary component, the model relies on data being relatively stationary and linear to produce accurate predictions. When these assumptions are not met, the predictions may still be less accurate.
Moreover, even though neural networks are used in ARIMA-NN to handle the residuals, they are often limited in their scope and ability to capture complex, long-term dependencies without a substantial amount of training data and computational resources. This hybrid approach is generally more complex and resource-intensive than either ARIMA or neural networks alone, making it less practical for large datasets or high-frequency trading applications where speed is essential.
Hybrid models like ARIMA-NN illustrate the desire to bridge the gap between traditional statistical methods and modern machine learning techniques. However, by combining these two fundamentally different approaches, hybrid models often face the limitations of both, without fully overcoming either. They remain constrained by ARIMA’s linear assumptions and preprocessing requirements while also introducing the neural network’s need for extensive training data. As a result, while hybrid models offer some improvement over traditional methods, they often fall short in capturing the full complexity of stock market data.