Analyzing Financial Health and Performance: A Multi-Sector Stock Deep Dive
A comprehensive examination of 10 companies across five key sectors, utilizing financial ratios and risk metrics to inform investment decisions.
Download source code using the link at the end of this article.
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScalerThis Python code imports several libraries crucial for financial data analysis, manipulation, numerical computation, and visualization. The yfinance library, imported as yf, facilitates downloading historical market data from Yahoo Finance. Pandas (imported as pd) provides the DataFrame structure, a powerful tool for organizing and manipulating data efficiently. NumPy (imported as np) underpins numerical computation, offering efficient array and matrix operations. Matplotlib's pyplot module (imported as plt) is used for creating visualizations. Finally, StandardScaler from scikit-learn's preprocessing module is imported for data standardization, a preprocessing step often essential for optimal performance in machine learning algorithms. This standardization centers the data around a mean of 0 and scales it to a standard deviation of 1, preventing features with larger magnitudes from disproportionately influencing analysis.
In summary, this code snippet imports the necessary tools for a program likely designed to download financial data, process and analyze it using pandas and NumPy's numerical capabilities, and visualize the results using Matplotlib. The inclusion of StandardScaler hints at a potential machine learning or statistical modeling component where standardized data is beneficial. The code itself, however, only imports these libraries; the actual data processing and analysis will be performed in subsequent code sections.
This analysis examines the historical stock performance of ten companies spanning five sectors. The objective is to calculate key financial ratios and derive insights into each company's performance, risk profile, and valuation, ultimately informing investment decisions.
We select two stocks from each of five key economic sectors: technology, healthcare, finance, consumer goods, and industrials.
Data collection is the initial phase.
stocks = ['AAPL', 'MSFT', 'JNJ', 'PFE', 'JPM', 'GS', 'TSLA', 'AMZN', 'DAL', 'HON' ]
start_date = '2018-09-01'
end_date = '2024-09-01'
stock_data = yf.download(stocks, start = start_date, end = end_date)
stock_data.head()[*********************100%***********************] 10 of 10 completedPrice Adj Close \
Ticker AAPL AMZN DAL GS
Date
2018-09-04 00:00:00+00:00 54.398647 101.975502 55.862934 206.222473
2018-09-05 00:00:00+00:00 54.043709 99.740997 54.278503 206.135681
2018-09-06 00:00:00+00:00 53.145641 97.915497 53.547958 203.497818
2018-09-07 00:00:00+00:00 52.716862 97.603500 53.946442 202.968475
2018-09-10 00:00:00+00:00 52.009350 96.950500 54.610577 201.233063
Price \
Ticker HON JNJ JPM MSFT
Date
2018-09-04 00:00:00+00:00 135.128784 113.395767 96.553993 105.049080
2018-09-05 00:00:00+00:00 136.948730 115.210487 96.084427 102.021049
2018-09-06 00:00:00+00:00 138.827835 116.066971 95.673584 102.256165
2018-09-07 00:00:00+00:00 137.812073 116.448586 95.858025 101.757759
2018-09-10 00:00:00+00:00 138.286102 116.355339 95.346550 102.858002
Price ... Volume \
Ticker PFE TSLA ... AAPL AMZN
Date ...
2018-09-04 00:00:00+00:00 30.788761 19.263332 ... 109560400 114422000
2018-09-05 00:00:00+00:00 31.145994 18.716000 ... 133332000 164412000
2018-09-06 00:00:00+00:00 31.093891 18.730000 ... 137160000 149774000
2018-09-07 00:00:00+00:00 31.406477 17.549334 ... 150479200 97852000
2018-09-10 00:00:00+00:00 31.302277 19.033333 ... 158066000 90896000
Price \
Ticker DAL GS HON JNJ JPM
Date
2018-09-04 00:00:00+00:00 5017400 2083500 2437270 4406800 10174200
2018-09-05 00:00:00+00:00 9495500 2092000 3343004 6174800 11462400
2018-09-06 00:00:00+00:00 7618100 2651400 4265119 6562000 9877600
2018-09-07 00:00:00+00:00 6307600 1952900 2886955 6375200 10955600
2018-09-10 00:00:00+00:00 3894900 1948100 2426941 4892200 8276900
Price
Ticker MSFT PFE TSLA
Date
2018-09-04 00:00:00+00:00 22634600 15274779 125257500
2018-09-05 00:00:00+00:00 32872400 21819908 115812000
2018-09-06 00:00:00+00:00 23477600 18356780 112212000
2018-09-07 00:00:00+00:00 22498600 21221658 337378500
2018-09-10 00:00:00+00:00 20727900 21482206 214252500
[5 rows x 60 columns]This Python code snippet downloads historical stock data. A list named stocks is created, containing stock tickers such as AAPL, MSFT, and JNJ, representing the companies whose stock price history will be retrieved. The start_date and end_date variables define the data retrieval period, in this case, from September 1st, 2018, to September 1st, 2024.
The core functionality is provided by the yf.download() function, from the yfinance library (requiring installation via pip install yfinance). This function fetches historical stock data from a financial data provider, likely Yahoo Finance. It uses the stocks list to specify which stocks to download, and the start and end variables to define the date range. The downloaded data includes daily open, high, low, close, adjusted close prices, and volume for each specified stock.
The retrieved data is stored in the stock_data variable, likely in a tabular format similar to a spreadsheet, with columns representing stock metrics (open, high, low, close, etc.) and rows representing individual trading days. The stock_data.head() method then displays the first few rows of this data, enabling a quick verification of successful data download and providing a preview of its structure. This serves as a valuable debugging and exploratory tool.
In summary, this code acts as a data acquisition module, efficiently retrieving and preparing historical stock market data for further analysis. Subsequent operations might include return calculations, statistical analysis, or data visualization using plotting libraries, all performed on the stock_data variable.
Data processing
stock_data.isna().sum()Price Ticker
Adj Close AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
Close AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
High AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
Low AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
Open AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
Volume AAPL 0
AMZN 0
DAL 0
GS 0
HON 0
JNJ 0
JPM 0
MSFT 0
PFE 0
TSLA 0
dtype: int64This Python code uses the pandas library to analyze missing data in a DataFrame. We assume stock_data is a pandas DataFrame, a tabular data structure with rows and columns. Each column represents a variable (e.g., stock price, date, volume), and each row represents an observation (e.g., a day's stock data).
The code, stock_data.isna().sum(), performs these steps: First, the .isna() method identifies missing data points (NaN values) within the DataFrame. This creates a new DataFrame of the same dimensions, where each element is a Boolean value (True for NaN, False otherwise). Second, the .sum() method is applied to this Boolean DataFrame. For each column, it sums the True values, effectively counting the number of NaN values in that column. The result is a pandas Series. The Series index consists of the original DataFrame's column names, and each value represents the count of missing data points in the corresponding column. This provides a concise summary of missing data per variable in the dataset.
The dataset contains no missing values.
adj_close = stock_data['Adj Close']
adj_close.head()Ticker AAPL AMZN DAL GS \
Date
2018-09-04 00:00:00+00:00 54.398647 101.975502 55.862934 206.222473
2018-09-05 00:00:00+00:00 54.043709 99.740997 54.278503 206.135681
2018-09-06 00:00:00+00:00 53.145641 97.915497 53.547958 203.497818
2018-09-07 00:00:00+00:00 52.716862 97.603500 53.946442 202.968475
2018-09-10 00:00:00+00:00 52.009350 96.950500 54.610577 201.233063
Ticker HON JNJ JPM MSFT \
Date
2018-09-04 00:00:00+00:00 135.128784 113.395767 96.553993 105.049080
2018-09-05 00:00:00+00:00 136.948730 115.210487 96.084427 102.021049
2018-09-06 00:00:00+00:00 138.827835 116.066971 95.673584 102.256165
2018-09-07 00:00:00+00:00 137.812073 116.448586 95.858025 101.757759
2018-09-10 00:00:00+00:00 138.286102 116.355339 95.346550 102.858002
Ticker PFE TSLA
Date
2018-09-04 00:00:00+00:00 30.788761 19.263332
2018-09-05 00:00:00+00:00 31.145994 18.716000
2018-09-06 00:00:00+00:00 31.093891 18.730000
2018-09-07 00:00:00+00:00 31.406477 17.549334
2018-09-10 00:00:00+00:00 31.302277 19.033333This Python code snippet processes financial data, specifically the adjusted closing prices of a stock. The code assumes the existence of a variable, stock_data, which is likely a Pandas DataFrame containing various stock performance metrics over time. Each row in this DataFrame represents a trading day, and columns represent metrics such as opening price, high, low, closing price, volume, and adjusted closing price.
The expression stock_data['Adj Close'] selects the column named 'Adj Close', representing the adjusted closing price. This adjusted price accounts for corporate actions like stock splits and dividends, offering a more reliable historical comparison of the stock's value.
The result of this selection is a Pandas Series—a single column from the DataFrame—containing a sequence of adjusted closing prices, each implicitly linked to a specific date.
The .head() method, applied to this Series, displays the first few (usually five) entries. This provides a quick visual check of the extracted data, confirming its accuracy and offering an initial impression of price trends. Essentially, it offers a preview of the adjusted closing price data.
In summary, the code extracts the adjusted closing prices from a comprehensive stock dataset and displays the first few entries, providing a concise view of a portion of the stock's price history. The code's functionality relies on the Pandas library, a powerful Python tool for data manipulation and analysis.
daily_returns = adj_close.pct_change()
cumulative_returns = (1 + daily_returns).cumprod()
daily_returns.dropna(inplace=True)
cumulative_returns.dropna(inplace=True)This Python code calculates and cleans cumulative investment returns from a time series of an asset's daily adjusted closing prices. The input is assumed to be a variable named adj_close, containing adjusted closing prices. "Adjusted" signifies that these prices account for corporate actions like stock splits and dividends, ensuring a consistent price history for analysis.
The daily percentage change in these adjusted closing prices is calculated using the expression adj_close.pct_change(). This function, typically from a library like Pandas, computes the percentage difference between each price and its predecessor. For instance, with closing prices of 100, 102, and 105, the daily returns would be 2% ( (102-100)/100 ) and 2.94% ( (105-102)/102 ), representing the daily percentage gain or loss.
Next, cumulative returns are computed as (1 + daily_returns).cumprod(). Adding 1 to each daily return accounts for the initial investment. The cumprod() function then calculates the cumulative product of these values; each daily return (plus 1) is multiplied by the cumulative product of all preceding daily returns. This yields a series reflecting the total return from the start of the period up to each day. For example, with daily returns of 2%, 3%, and -1%, the cumulative returns would be 1.02, 1.02 * 1.03 = 1.0506, and 1.0506 * 0.99 = 1.040094, illustrating investment growth over time.
Finally, the code removes missing values (NaN, or "Not a Number") from both the daily_returns and cumulative_returns series using the expression dropna(inplace=True). The dropna() function performs this data cleaning operation, and the inplace=True argument modifies the original series directly rather than creating new ones. These missing values, often present at the beginning of the time series due to a lack of preceding data for comparison, are removed to ensure accurate subsequent calculations and analysis.
In conclusion, this code snippet processes a series of adjusted closing prices to generate clean daily and cumulative return series suitable for further financial analysis, such as performance and risk assessment.
daily_returns.head()Ticker AAPL AMZN DAL GS HON \
Date
2018-09-05 00:00:00+00:00 -0.006525 -0.021912 -0.028363 -0.000421 0.013468
2018-09-06 00:00:00+00:00 -0.016617 -0.018302 -0.013459 -0.012797 0.013721
2018-09-07 00:00:00+00:00 -0.008068 -0.003186 0.007442 -0.002601 -0.007317
2018-09-10 00:00:00+00:00 -0.013421 -0.006690 0.012311 -0.008550 0.003440
2018-09-11 00:00:00+00:00 0.025283 0.024827 0.012335 -0.007330 -0.001897
Ticker JNJ JPM MSFT PFE TSLA
Date
2018-09-05 00:00:00+00:00 0.016003 -0.004863 -0.028825 0.011603 -0.028413
2018-09-06 00:00:00+00:00 0.007434 -0.004276 0.002305 -0.001673 0.000748
2018-09-07 00:00:00+00:00 0.003288 0.001928 -0.004874 0.010053 -0.063036
2018-09-10 00:00:00+00:00 -0.000801 -0.005336 0.010812 -0.003318 0.084562
2018-09-11 00:00:00+00:00 0.009474 0.006332 0.017005 0.005944 -0.021226This Python code uses the head() method on a Pandas DataFrame named daily_returns. Pandas is a Python library for data manipulation and analysis. A Pandas DataFrame is a two-dimensional data structure, analogous to a spreadsheet or table, with rows and columns. In this context, daily_returns likely contains daily financial return data, such as the percentage change in a stock or index price each day. Each row represents a single day, and columns might include the date, the return value, and other relevant data.
The head() method is a Pandas DataFrame function for quickly inspecting DataFrame contents, particularly large ones. Calling head() on a DataFrame displays the first few rows—by default, the first five. This provides a quick overview of the data structure, column names, and sample values, avoiding the output of an entire, potentially very large, DataFrame.
Therefore, daily_returns.head() displays the first five rows of the daily_returns DataFrame, offering a concise data preview. This is a valuable tool for data exploration and verification in data analysis. To view a different number of rows, specify the desired number as an argument; for instance, daily_returns.head(10) displays the first ten rows.
cumulative_returns.head()Ticker AAPL AMZN DAL GS HON \
Date
2018-09-05 00:00:00+00:00 0.993475 0.978088 0.971637 0.999579 1.013468
2018-09-06 00:00:00+00:00 0.976966 0.960186 0.958560 0.986788 1.027374
2018-09-07 00:00:00+00:00 0.969084 0.957127 0.965693 0.984221 1.019857
2018-09-10 00:00:00+00:00 0.956078 0.950723 0.977582 0.975806 1.023365
2018-09-11 00:00:00+00:00 0.980250 0.974327 0.989640 0.968653 1.021424
Ticker JNJ JPM MSFT PFE TSLA
Date
2018-09-05 00:00:00+00:00 1.016003 0.995137 0.971175 1.011603 0.971587
2018-09-06 00:00:00+00:00 1.023556 0.990882 0.973413 1.009910 0.972314
2018-09-07 00:00:00+00:00 1.026922 0.992792 0.968669 1.020063 0.911023
2018-09-10 00:00:00+00:00 1.026099 0.987495 0.979142 1.016679 0.988060
2018-09-11 00:00:00+00:00 1.035821 0.993747 0.995793 1.022722 0.967088This Python code uses the pandas library to display the first five rows of a DataFrame called cumulative_returns. Pandas is a data analysis library; a DataFrame is a tabular data structure similar to a spreadsheet or SQL table, with rows and columns. In this context, the cumulative_returns DataFrame likely contains investment return data. Each row might represent a time period (e.g., a day or a month), and each column might represent a different aspect of the returns, such as the return for a specific asset or portfolio. The term "cumulative" indicates that the returns are accumulated over time, with each value representing the total return up to that point.
The head() method is a pandas function for quickly previewing a DataFrame's contents. Calling cumulative_returns.head() without arguments displays the first five rows, providing a quick overview of the data's structure and values. To display a different number of rows, specify that number as an argument; for example, cumulative_returns.head(10) would show the first ten rows.
Therefore, cumulative_returns.head() offers a concise way to inspect the initial portion of the cumulative_returns DataFrame, facilitating a quick check of the data format and values before more extensive analysis. Using head() or its counterpart, tail(), for initial data inspection is standard practice in data analysis.
Financial Ratios
The price-to-earnings (P/E) ratio is a valuation metric that compares a company's current market price per share to its earnings per share. A high P/E ratio often suggests that investors anticipate significant future growth, while a low P/E ratio may indicate that the market perceives the company as undervalued.
The Price-to-Book (P/B) ratio assesses a company's market valuation relative to its book value. A high P/B ratio may indicate overvaluation, whereas a low P/B ratio might suggest undervaluation.
The debt-to-equity (D/E) ratio is a metric assessing a company's financial leverage. It's calculated by dividing total liabilities by shareholders' equity. A higher D/E ratio signifies greater reliance on debt financing, indicating increased financial risk.
Return on Equity (ROE) measures a company's profitability by comparing its net income to its shareholders' equity. A higher ROE signifies a more efficient utilization of shareholder equity in generating profits.
EPS growth quantifies the change in earnings per share over time. A positive EPS growth rate signifies increasing profitability.
def get_financial_ratios(stocks):
ratios = pd.DataFrame(index=stocks, columns=['P/E', 'P/B', 'D/E', 'ROE', 'EPS Growth'])
for stock in stocks:
ticker = yf.Ticker(stock)
info = ticker.info
ratios.loc[stock, 'P/E'] = info.get('trailingPE', np.nan)
ratios.loc[stock, 'P/B'] = info.get('priceToBook', np.nan)
ratios.loc[stock, 'D/E'] = info.get('debtToEquity', np.nan)
ratios.loc[stock, 'ROE'] = info.get('returnOnEquity', np.nan)
ratios.loc[stock, 'EPS Growth'] = info.get('earningsGrowth', np.nan)
return ratios
financial_ratios = get_financial_ratios(stocks)
financial_ratiosP/E P/B D/E ROE EPS Growth
AAPL 33.35671 49.936104 151.862 1.60583 0.111
MSFT 34.994926 11.443724 36.447 0.37133 0.097
JNJ 25.304083 5.627292 57.999 0.22146 -0.016
PFE NaN 1.911773 79.407 -0.02737 -0.982
JPM 11.41662 1.839256 NaN 0.16545 0.288
GS 15.059673 1.466998 585.382 0.0949 1.793
TSLA 62.498592 10.661701 18.606 0.20861 -0.462
AMZN 42.32458 7.86779 66.756 0.21933 0.938
DAL 6.202296 2.238157 209.196 0.43806 -0.292
HON 22.760546 7.651997 165.725 0.3274 0.063This Python code calculates key financial ratios for a list of stocks. The core functionality is encapsulated within a function, get_financial_ratios, which accepts a list of stock tickers as input. This function initializes a Pandas DataFrame, a structured data container analogous to a spreadsheet, to store the calculated ratios. The DataFrame is pre-configured with columns for Price-to-Earnings (P/E), Price-to-Book (P/B), Debt-to-Equity (D/E), Return on Equity (ROE), and EPS Growth, and rows representing each input stock. Missing data is represented by np.nan.
The code iterates through each stock ticker. For each ticker, it uses the yfinance library to retrieve financial data via yf.Ticker().info, which returns a dictionary containing various financial metrics. The function then extracts the desired ratios from this dictionary using the .get() method. This method provides robust error handling; if a ratio is unavailable for a given stock, .get() returns np.nan instead of raising an error. These extracted ratios are then inserted into the corresponding cells of the ratios DataFrame using .loc[], which allows for data access by row label (stock ticker) and column name (ratio).
After processing all stocks, the function returns the complete ratios DataFrame. The main part of the code calls get_financial_ratios with a list of stocks (assumed to be defined elsewhere), assigning the returned DataFrame to the variable financial_ratios. The final line, financial_ratios, likely displays this DataFrame within an interactive environment like a Jupyter Notebook, presenting the calculated ratios for each stock.
In summary, this code offers an efficient and robust method for retrieving and organizing multiple financial ratios for a group of stocks, facilitating financial analysis. The use of Pandas enhances data handling and readability, while the error handling mechanisms ensure the code's reliability.
Initial observations
Apple Inc. (AAPL) and Microsoft Corp. (MSFT) are prominent technology companies exhibiting substantial growth potential, as evidenced by their elevated price-to-earnings (P/E) ratios of 33.36 and 34.99, respectively. Apple's high return on equity (ROE) of 1.61 suggests strong profitability; however, its comparatively high debt-to-equity (D/E) ratio indicates considerable financial leverage. In contrast, Microsoft displays a more conservative D/E ratio of 36.45, reflecting greater financial stability, although its ROE of 0.37 is lower than Apple's, suggesting less profitability.
Johnson & Johnson (JNJ) and Pfizer Inc. (PFE) are considered stable investments in the healthcare sector. JNJ exhibits steady performance, indicated by a moderate price-to-earnings ratio (P/E) of 25.30 and a robust return on equity (ROE) of 0.22. However, negative earnings per share (EPS) growth presents a cause for concern. Pfizer's low price-to-book ratio (P/B) suggests potential undervaluation; however, its negative EPS growth and ROE are significant drawbacks.
JPMorgan Chase (JPM) and Goldman Sachs (GS) exhibit contrasting financial profiles. JPMorgan's low price-to-earnings (P/E) ratio and stable return on equity (ROE) suggest a potential undervaluation. Conversely, Goldman Sachs' high P/E ratio and significantly high debt-to-equity (D/E) ratio indicate considerable leverage and associated risk. However, Goldman Sachs also demonstrates robust earnings per share (EPS) growth.
Tesla Inc. (TSLA) and Amazon.com Inc. (AMZN) are viewed as companies with significant growth potential. Tesla's high price-to-earnings (P/E) and price-to-book (P/B) ratios suggest the market anticipates substantial future growth. However, Tesla's negative earnings per share (EPS) growth raises some concerns. Conversely, Amazon's robust EPS growth, coupled with a high P/E ratio, reflects a positive market sentiment. Amazon's debt-to-equity (D/E) ratio appears manageable, further supporting this positive outlook.
Delta Air Lines (DAL) and Honeywell International Inc. (HON) offer distinct investment profiles. Delta's low price-to-earnings ratio suggests potential undervaluation; however, its high debt-to-equity ratio and negative earnings per share growth represent significant risks. Honeywell, on the other hand, exhibits a more moderate price-to-earnings ratio and a strong return on equity, indicating greater financial stability. Nevertheless, Honeywell's high debt-to-equity ratio also presents a potential risk factor.
Exploratory Data Analysis
To facilitate a clearer analysis of trends, we will standardize the stock prices.
scaler = StandardScaler()
stan_adj_close = pd.DataFrame(scaler.fit_transform(adj_close),
index=adj_close.index,
columns=adj_close.columns)
stan_adj_close.head()Ticker AAPL AMZN DAL GS HON \
Date
2018-09-04 00:00:00+00:00 -1.355941 -0.841165 1.533257 -0.835585 -1.468274
2018-09-05 00:00:00+00:00 -1.362734 -0.906108 1.361041 -0.836559 -1.402479
2018-09-06 00:00:00+00:00 -1.379922 -0.959163 1.281636 -0.866171 -1.334546
2018-09-07 00:00:00+00:00 -1.388129 -0.968230 1.324948 -0.872113 -1.371267
2018-09-10 00:00:00+00:00 -1.401670 -0.987209 1.397135 -0.891594 -1.354130
Ticker JNJ JPM MSFT PFE TSLA
Date
2018-09-04 00:00:00+00:00 -1.651809 -0.894918 -1.462677 -0.512222 -1.386767
2018-09-05 00:00:00+00:00 -1.548253 -0.909257 -1.494497 -0.458429 -1.391959
2018-09-06 00:00:00+00:00 -1.499379 -0.921802 -1.492026 -0.466275 -1.391826
2018-09-07 00:00:00+00:00 -1.477603 -0.916170 -1.497264 -0.419205 -1.403025
2018-09-10 00:00:00+00:00 -1.482924 -0.931789 -1.485702 -0.434896 -1.388949This Python code snippet demonstrates data scaling using standardization, a common preprocessing technique in machine learning. The code utilizes the StandardScaler class, typically from the scikit-learn library. StandardScaler transforms data so each feature—represented as a column in a dataset—has a mean of 0 and a standard deviation of 1. This centering and normalization is crucial for many machine learning algorithms, improving their performance by preventing features with larger magnitudes from disproportionately influencing the model.
First, a StandardScaler object is created: scaler = StandardScaler(). This object will be used to perform the standardization.
Next, a Pandas DataFrame, stan_adj_close, is created to store the scaled data. Pandas is a Python library for data manipulation and analysis; a DataFrame is a tabular data structure. The data for this DataFrame comes from the application of the StandardScaler to existing data.
The core scaling operation is performed by scaler.fit_transform(adj_close). The input, adj_close, is assumed to be a Pandas DataFrame containing numerical data—likely adjusted closing prices of stocks or similar time series data. The fit_transform method performs two key steps:
First, fit() analyzes adj_close, calculating the mean and standard deviation for each column (feature). This establishes the parameters needed for the subsequent transformation.
Second, transform() applies the standardization formula— (x - mean) / standard deviation—to each data point (x) in adj_close, using the means and standard deviations calculated in the fit() step.
The resulting array from fit_transform is then converted into a Pandas DataFrame. The original index and column names from adj_close are preserved using index=adj_close.index and columns=adj_close.columns, respectively.
Finally, stan_adj_close.head() displays the first few rows of the newly created DataFrame, providing a quick visual check of the standardized data.
In summary, this code snippet standardizes a dataset (adj_close) using StandardScaler, storing the result in a new DataFrame (stan_adj_close) for subsequent use in machine learning algorithms. Standardization ensures that features contribute equally to model calculations, preventing bias from features with differing scales or magnitudes.
print("Means:\n", stan_adj_close.mean())
print("Standard Deviations:\n", stan_adj_close.std())Means:
Ticker
AAPL 7.538915e-17
AMZN -1.884729e-16
DAL -3.769457e-16
GS 1.507783e-16
HON -1.507783e-16
JNJ 7.538915e-17
JPM -1.507783e-16
MSFT -7.538915e-17
PFE -1.884729e-16
TSLA 1.507783e-16
dtype: float64
Standard Deviations:
Ticker
AAPL 1.000332
AMZN 1.000332
DAL 1.000332
GS 1.000332
HON 1.000332
JNJ 1.000332
JPM 1.000332
MSFT 1.000332
PFE 1.000332
TSLA 1.000332
dtype: float64This Python code calculates and displays the mean and standard deviation of a numerical dataset. The dataset, represented by the variable stan_adj_close, is assumed to be a collection of numbers such as a list or a column from a spreadsheet, perhaps containing adjusted stock closing prices. The code’s functionality relies on this numerical dataset, although the specific method of creating stan_adj_close is not shown.
The code utilizes the .mean() and .std() methods, likely provided by a Python data analysis library like Pandas or NumPy. These methods efficiently handle numerical data computations.
The .mean() method computes the average of all values in stan_adj_close by summing the values and dividing by their count. The result is a single number representing the data’s central tendency.
The .std() method calculates the standard deviation, a measure of data dispersion or variation. A low standard deviation indicates data points clustered near the mean, while a high standard deviation shows data spread across a wider range. It quantifies the deviation of individual data points from the average.
The print() function displays the calculated mean and standard deviation. Newline characters (\n) are included to enhance readability, resulting in the output being formatted as:
Means: [the calculated mean]
Standard Deviations: [the calculated standard deviation]
In short, this code efficiently computes and presents descriptive statistics — the mean and standard deviation — for a numerical dataset, providing a concise summary of the data’s central tendency and variability.
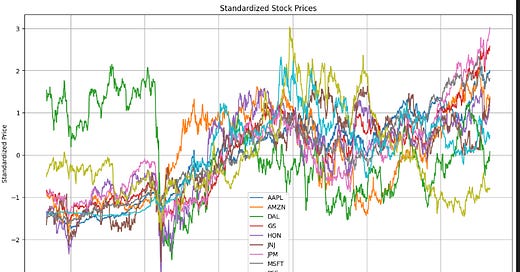
# Plot standardized adjusted close prices
plt.figure(figsize=(14, 8))
for stock in stan_adj_close.columns:
plt.plot(stan_adj_close.index, stan_adj_close[stock], label=stock)
plt.title('Standardized Stock Prices')
plt.xlabel('Date')
plt.ylabel('Standardized Price')
plt.legend(loc='best')
plt.grid(True)
plt.show()This Python code generates a plot visualizing the standardized adjusted closing prices of multiple stocks over time. The code begins by implicitly importing the matplotlib.pyplot library, evidenced by the use of functions like plt.figure and plt.plot.
A figure is created using plt.figure(figsize=(14, 8)), specifying dimensions of 14 inches by 8 inches for improved readability.
The core plotting logic resides within a for loop: for stock in stan_adj_close.columns:. This loop iterates through each column of the stan_adj_close Pandas DataFrame, where each column represents a different stock. The column name is used as a label for the corresponding plot line.
Inside the loop, plt.plot(stan_adj_close.index, stan_adj_close[stock], label=stock) plots the data. stan_adj_close.index provides the dates (the DataFrame’s index), and stan_adj_close[stock] represents the standardized adjusted closing prices for the current stock. The label parameter ensures each line is clearly identified in the legend.
Following the loop, several enhancements improve the plot’s clarity. plt.title(‘Standardized Stock Prices’) sets the plot title. plt.xlabel(‘Date’) and plt.ylabel(‘Standardized Price’) label the axes. plt.legend(loc=’best’) automatically positions the legend optimally. plt.grid(True) adds a grid for easier data interpretation. Finally, plt.show() displays the generated plot.
In essence, the code processes a DataFrame containing standardized adjusted closing prices. Standardization implies preprocessing to achieve a mean of 0 and a standard deviation of 1, facilitating comparison across stocks with varying price scales. The term “adjusted close” indicates prices adjusted for corporate actions (e.g., stock splits, dividends), offering a more accurate historical performance representation. The code iterates through each stock, plots its price history, and presents the complete plot with informative labels and a legend.
# Plot Cumulative Returns
plt.figure(figsize=(12, 6))
for stock in stocks:
plt.plot(cumulative_returns.index, cumulative_returns[stock], label=stock)
plt.title('Cumulative Return (2018-2024)')
plt.xlabel('Date')
plt.ylabel('Cumulative Return')
plt.legend()
plt.show()This Python code generates a graph visualizing the cumulative returns of multiple stocks over time. The code first establishes the plotting environment using the matplotlib.pyplot library, imported as plt. A figure is created with dimensions 12 inches by 6 inches using plt.figure(figsize=(12, 6)), ensuring sufficient readability.
The code then iterates through a list named stocks, presumably containing stock symbols such as “AAPL” or “MSFT”. The for stock in stocks: loop processes each stock individually.
Within the loop, the core plotting function plt.plot(cumulative_returns.index, cumulative_returns[stock], label=stock) is executed. cumulative_returns is a Pandas DataFrame containing the cumulative returns for each stock; its index represents the dates, and cumulative_returns[stock] accesses the column corresponding to a specific stock. The plot function generates a line graph, with the dates on the x-axis and cumulative returns on the y-axis. The label=stock argument assigns a unique label to each line, facilitating identification in the legend.
After processing all stocks, plt.title(‘Cumulative Return (2018–2024)’) sets the graph’s title, indicating the time period. The x and y axes are labeled using plt.xlabel(‘Date’) and plt.ylabel(‘Cumulative Return’), respectively. plt.legend() displays the legend, and plt.show() renders the complete graph.
In summary, this code leverages Pandas for data manipulation and Matplotlib for visualization. The code iteratively plots the cumulative returns of each stock from the Pandas DataFrame onto a single graph, providing a comparative analysis of their performance over the specified period (2018–2024). The integration of Pandas and Matplotlib creates a clear and informative visual representation of the data.
Moving Averages
def calculate_moving_averages(df, windows=[50, 200]):
ma_data = pd.DataFrame(index=df.index)
for window in windows:
for ticker in df['Adj Close'].columns:
ma_data[f'{ticker}_MA{window}'] = df['Adj Close'][ticker].rolling(window=window).mean()
return ma_data
# Calculate moving averages
ma_data = calculate_moving_averages(stock_data)
# Define the number of stocks and create subplots
num_stocks = len(stock_data['Adj Close'].columns)
fig, axes = plt.subplots(nrows=num_stocks, ncols=1, figsize=(15, 5 * num_stocks), sharex=True)
# Plot data
for i, ticker in enumerate(stock_data['Adj Close'].columns):
ax = axes[i]
ax.plot(stock_data.index, stock_data['Adj Close'][ticker], color = 'black', label=f'{ticker} Price')
ax.plot(ma_data.index, ma_data[f'{ticker}_MA50'], label=f'{ticker} 50-day MA', linestyle='-', color = 'blue')
ax.plot(ma_data.index, ma_data[f'{ticker}_MA200'], label=f'{ticker} 200-day MA', linestyle='-', color = 'red')
ax.set_title(f'{ticker} Stock Price with Moving Averages')
ax.set_xlabel('Date')
ax.set_ylabel('Price')
ax.legend()
plt.tight_layout()
plt.show()This Python code calculates and plots 50-day and 200-day moving averages for stock prices. The code first defines a function, calculate_moving_averages, which accepts a Pandas DataFrame as input. This DataFrame, assumed to contain stock price data, is referred to as df. The function also takes a windows parameter, specifying the lengths of the moving averages to calculate; it defaults to 50 and 200 days. The function iterates through each specified window size and each stock ticker found in the DataFrames Adj Close column, presumed to contain adjusted closing prices. For each combination, it computes the moving average using a rolling mean calculation. The resulting DataFrame, ma_data, contains the calculated moving averages; column names clearly identify the stock and moving average (for example, AAPL_MA50 represents Apple’s 50-day moving average).
Next, the code calls calculate_moving_averages with a DataFrame called stock_data, presumably loaded from an external file or database (not shown here). This generates the ma_data DataFrame containing the moving averages.
The plotting section determines the number of stocks and uses Matplotlib to create subplots, one for each stock, to display each stock’s price and moving averages individually. The figsize argument adjusts the overall plot size, and sharex=True ensures the x-axis (representing date) is shared across all subplots.
The code then iterates through each stock, plotting the original adjusted closing price (‘Adj Close’) as a black line, the 50-day moving average as a blue line, and the 200-day moving average as a red line on each subplot. Each subplot is titled with the stock ticker, and axis labels and a legend are added. plt.tight_layout() optimizes subplot parameters for better visual presentation, preventing overlapping elements, and plt.show() displays the resulting plot.
In summary, this code processes stock price data to compute and visualize 50-day and 200-day moving averages for multiple stocks. Pandas facilitates efficient data manipulation, while Matplotlib provides the visualization capabilities. This common technical analysis technique helps identify trends and potential trading signals.
correlation_matrix = adj_close.pct_change().corr()
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Heatmap of Stock Returns')
plt.show()This Python code generates and visualizes a correlation heatmap of stock returns. The code begins with a Pandas DataFrame, adj_close, containing the adjusted closing prices of multiple stocks. Each column represents a stock, and each row represents a day’s closing price.
The percentage change in adjusted closing prices is calculated using adj_close.pct_change(), transforming the price data into daily returns. Positive values signify price increases, while negative values indicate decreases.
The correlation matrix of these daily returns is then computed using .corr(). This matrix is a square table; each cell (i, j) represents the correlation coefficient between the returns of stock i and stock j. A value of 1 denotes perfect positive correlation (both stocks move in the same direction), -1 indicates perfect negative correlation (stocks move in opposite directions), and 0 signifies no linear correlation.
A Matplotlib figure is created with a size of 12 inches wide and 10 inches tall using plt.figure(figsize=(12, 10)). This figure serves as the canvas for the heatmap.
The heatmap itself is generated using Seaborn’s heatmap function: sns.heatmap(correlation_matrix, annot=True, cmap=’coolwarm’). The correlation matrix provides the data. annot=True displays the correlation coefficients directly on the heatmap. The ‘coolwarm’ colormap uses cool colors (blues) for negative correlations and warm colors (reds) for positive correlations.
A title, ‘Correlation Heatmap of Stock Returns’, is added using plt.title(‘Correlation Heatmap of Stock Returns’).
Finally, plt.show() displays the generated heatmap.
In summary, the code processes adjusted closing stock prices to calculate daily returns and subsequently computes the correlation between the returns of different stocks. This correlation is then visualized using a color-coded heatmap, clearly showing which stocks tend to move together or inversely. Seaborn enhances the visualization, providing a more informative and visually appealing result compared to a basic Matplotlib heatmap.
Risk assessment.
This section calculates the annualized volatility for each stock.
volatility = daily_returns.std() * np.sqrt(252)
print("Annualised Volatility")
print(volatility)Annualised Volatility
Ticker
AAPL 0.317758
AMZN 0.354795
DAL 0.455136
GS 0.316769
HON 0.258063
JNJ 0.198183
JPM 0.303579
MSFT 0.297460
PFE 0.262012
TSLA 0.643344
dtype: float64This Python code computes the annualized volatility of a financial asset, such as a stock. The calculation relies on a pre-existing variable, daily_returns, which contains a sequence of daily percentage price changes. For instance, a price increase from $100 to $102 represents a 2% daily return. The NumPy library (referred to as np) is used for numerical computation.
The core calculation is daily_returns.std() * np.sqrt(252). daily_returns.std() calculates the standard deviation of the daily returns. Standard deviation measures the dispersion of a dataset; a higher standard deviation indicates greater volatility, signifying more dramatic price fluctuations. In this context, it quantifies the typical daily price swing.
The term np.sqrt(252) calculates the square root of 252, an approximation of the number of trading days in a year. Multiplying the daily standard deviation by this factor annualizes the volatility. Standard deviation measures variation over a specific period; since our input is daily data, we scale it to an annual measure. The square root is used because variance (the square of the standard deviation) is additive across independent periods.
Therefore, the entire expression calculates the annualized volatility. It scales the daily standard deviation to represent the expected volatility over a year, assuming independent and identically distributed daily returns.
Finally, the code prints “Annualised Volatility” followed by the calculated value, providing a clear, interpretable result. This single number represents the expected annual price fluctuation of the asset, with higher values indicating higher risk.
Beta and Sharpe ratios are key metrics in portfolio management.
Beta measures a stock’s volatility relative to the overall market. A beta greater than one signifies that the stock’s price fluctuates more dramatically than the market average; conversely, a beta less than one indicates lower volatility than the market.
The Sharpe ratio quantifies risk-adjusted return. A higher Sharpe ratio denotes superior performance relative to the risk undertaken. Negative Sharpe ratios suggest that the investment’s returns are below the risk-free rate, indicating underperformance given the inherent risk.
def calculate_beta(stock_returns, market_returns):
covariance = stock_returns.cov(market_returns)
market_variance = market_returns.var()
return covariance / market_variance
def calculate_sharpe_ratio(returns, risk_free_rate = 0.037): # Current rate of 10 year Treasury Rate
excess_returns = returns - risk_free_rate / 252
return np.sqrt(252) * excess_returns.mean() / excess_returns.std()
# Get market data
sp500 = yf.download('^GSPC', start = start_date, end = end_date)
sp500_returns = sp500['Adj Close'].pct_change().dropna()
sp500_returns.index = sp500_returns.index.tz_localize(None)
risk_metrics = pd.DataFrame(index = stocks, columns = ['Beta', 'Sharpe Ratio'])
for stock in stocks:
stock_returns = daily_returns[stock].dropna()
stock_returns.index = stock_returns.index.tz_localize(None)
risk_metrics.loc[stock, 'Beta'] = calculate_beta(stock_returns, sp500_returns)
risk_metrics.loc[stock, 'Sharpe Ratio'] = calculate_sharpe_ratio(stock_returns)
risk_metrics.loc[stock, 'Annualized Volatility'] = stock_returns.std() * np.sqrt(252)
risk_metrics[*********************100%***********************] 1 of 1 completedBeta Sharpe Ratio Annualized Volatility
AAPL 1.222401 0.799211 0.317758
MSFT 1.198368 0.799902 0.297460
JNJ 0.504701 0.23341 0.198183
PFE 0.570414 -0.048572 0.262012
JPM 1.06364 0.495124 0.303579
GS 1.136924 0.519749 0.316769
TSLA 1.517683 0.889902 0.643344
AMZN 1.142806 0.336861 0.354795
DAL 1.256848 0.047701 0.455136
HON 0.945769 0.264842 0.258063This Python code calculates two key portfolio risk metrics: beta and the Sharpe ratio. The code first defines two functions, calculate_beta and calculate_sharpe_ratio.
The calculate_beta function computes a stock’s beta, a measure of its price volatility relative to the overall market. A beta of 1 signifies that the stock’s price moves in line with the market. A beta greater than 1 indicates higher volatility than the market, while a beta less than 1 suggests lower volatility. The function calculates this by dividing the covariance of the stock’s returns and the market’s returns by the market’s variance. Covariance measures the degree to which two variables change together, while variance quantifies the dispersion of a single variable’s data points.
The calculate_sharpe_ratio function calculates the Sharpe ratio, a measure of risk-adjusted return. It indicates the additional return achieved per unit of risk taken. The function determines excess returns by subtracting a risk-free rate — in this case, the annualized 10-year Treasury rate, scaled to a daily rate by dividing by 252 — from the stock’s returns. The average excess return is then divided by the standard deviation of the excess returns, a measure of risk. Finally, the result is annualized by multiplying by the square root of 252, assuming 252 trading days per year.
The main section of the code begins by downloading market data. It uses yf.download, likely from the yfinance library, to obtain historical adjusted closing prices for the S&P 500 index (‘^GSPC’). Daily returns for the S&P 500 are then calculated as the percentage change in adjusted closing prices. Time zone information is removed from the index to prevent potential complications.
An empty Pandas DataFrame, risk_metrics, is initialized to store the calculated beta and Sharpe ratio for each stock in a list named stocks.
The code iterates through each stock in the stocks list. For each stock, it retrieves daily returns, removes missing data using dropna(), and removes time zone information. The calculate_beta and calculate_sharpe_ratio functions are then called to compute the beta and Sharpe ratio, using the S&P 500 returns as the market benchmark. The annualized volatility of the stock’s returns (standard deviation multiplied by the square root of 252) is also calculated. All three metrics — beta, Sharpe ratio, and annualized volatility — are then stored in the risk_metrics DataFrame.
Finally, the code displays the risk_metrics DataFrame, summarizing the risk and return characteristics of each stock in the portfolio. The use of Pandas facilitates efficient data manipulation and storage. The defined functions enhance code reusability and readability.
Tesla (TSLA, beta 1.52) and Apple (AAPL, beta 1.22) exhibit the highest volatility relative to the market, suggesting a higher risk profile but also the potential for greater returns. Delta Air Lines (DAL, beta 1.26) and Goldman Sachs (GS, beta 1.14) also demonstrate above-average market volatility.
Conversely, Johnson & Johnson (JNJ, beta 0.50) and Honeywell International (HON, beta 0.95) display lower volatility compared to the market, indicating potentially more stable investment characteristics.
Analysis of the Sharpe ratio reveals that Tesla (TSLA, Sharpe ratio 0.89) and Microsoft (MSFT, Sharpe ratio 0.80) offer the highest risk-adjusted returns. In contrast, Pfizer (PFE, Sharpe ratio -0.05) and Johnson & Johnson (JNJ, Sharpe ratio 0.23) show lower Sharpe ratios, signifying weaker performance relative to their associated risk levels.
Recommendations
def get_recommendation(row):
score = 0
if row['P/E'] < 20: score += 1
if row['P/B'] < 3: score += 1
if row['D/E'] < 1: score += 1
if row['ROE'] > 0.15: score += 1
if row['EPS Growth'] > 0.1: score += 1
if 0.8 < row['Beta'] < 1.2: score += 1
if row['Sharpe Ratio'] > 1: score += 1
if score >= 5:
return 'Buy'
elif score >= 3:
return 'Hold'
else:
return 'Sell'
recommendations = pd.concat([financial_ratios, risk_metrics], axis=1)
recommendations['Recommendation'] = recommendations.apply(get_recommendation, axis=1)recommendationsP/E P/B D/E ROE EPS Growth Beta \
AAPL 33.35671 49.936104 151.862 1.60583 0.111 1.222401
MSFT 34.994926 11.443724 36.447 0.37133 0.097 1.198368
JNJ 25.304083 5.627292 57.999 0.22146 -0.016 0.504701
PFE NaN 1.911773 79.407 -0.02737 -0.982 0.570414
JPM 11.41662 1.839256 NaN 0.16545 0.288 1.06364
GS 15.059673 1.466998 585.382 0.0949 1.793 1.136924
TSLA 62.498592 10.661701 18.606 0.20861 -0.462 1.517683
AMZN 42.32458 7.86779 66.756 0.21933 0.938 1.142806
DAL 6.202296 2.238157 209.196 0.43806 -0.292 1.256848
HON 22.760546 7.651997 165.725 0.3274 0.063 0.945769 Sharpe Ratio Annualized Volatility Recommendation
AAPL 0.799211 0.317758 Sell
MSFT 0.799902 0.297460 Sell
JNJ 0.23341 0.198183 Sell
PFE -0.048572 0.262012 Sell
JPM 0.495124 0.303579 Buy
GS 0.519749 0.316769 Hold
TSLA 0.889902 0.643344 Sell
AMZN 0.336861 0.354795 Hold
DAL 0.047701 0.455136 Hold
HON 0.264842 0.258063 SellThis Python code implements a basic stock recommendation system. It uses financial and risk metrics, presumably from Pandas DataFrames named financial_ratios and risk_metrics, which are combined to create a recommendations DataFrame. The system assigns a buy, hold, or sell recommendation to each stock based on a scoring system.
The core logic resides in the get_recommendation function. This function accepts a single row of data representing a stock’s metrics and assigns a score based on several financial ratios and risk metrics. Specifically, it checks the Price-to-Earnings (P/E) ratio, Price-to-Book (P/B) ratio, Debt-to-Equity (D/E) ratio, Return on Equity (ROE), EPS Growth, Beta, and Sharpe Ratio against predefined thresholds. Each ratio meeting its threshold adds to the overall score. These thresholds are arbitrary and would need adjustment depending on the investment strategy and market conditions.
After evaluating all ratios, the function determines a recommendation based on the final score. A score of 5 or greater results in a ‘Buy’ recommendation; a score between 3 and 4 yields a ‘Hold’ recommendation; and a score below 3 results in a ‘Sell’ recommendation. This is a straightforward rule-based system; more sophisticated approaches might employ complex scoring or machine learning techniques.
The code first combines the financial_ratios and risk_metrics DataFrames column-wise into a single DataFrame called recommendations using pd.concat([financial_ratios, risk_metrics], axis=1). Then, it applies the get_recommendation function row-wise to the recommendations DataFrame using recommendations[‘Recommendation’] = recommendations.apply(get_recommendation, axis=1). This adds a new ‘Recommendation’ column containing the buy, hold, or sell recommendation for each stock.
Finally, the enhanced recommendations DataFrame, including the original financial and risk metrics plus the generated recommendations, is displayed.
This code provides a simplified stock screening and recommendation system. Its ease of understanding is a benefit, but its accuracy relies heavily on the chosen thresholds and the input data quality. A production-ready system would require far greater complexity, incorporating more sophisticated analysis, robust risk management, and potentially machine learning algorithms.