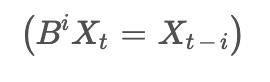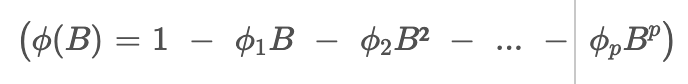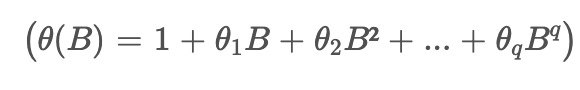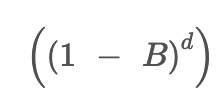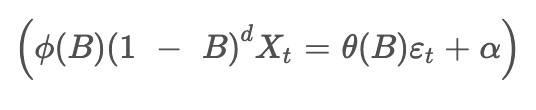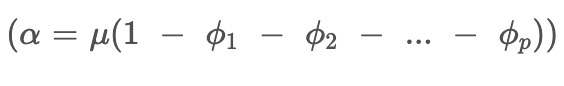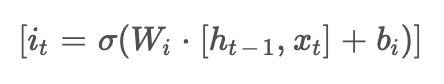Forecasting NVIDIA’s Stock with AI: A Study of Predictive Models
Evaluating the Performance of ARIMA, LSTM, MLP, and ARIMA-GARCH Models Over Five Years
A stock's future price must be predicted by financial institutions and investors. Due to its advances in artificial intelligence, NVIDIA has become a key player in machine learning fields. In our article, I focus on NVIDIA. I use ARIMA, MLP, LSTM, and a combined ARIMA-GARCH model among the models we are using.
Based on data from Yahoo Finance, I have analyzed NVIDIA stocks performance from April 12 2019 to April 11 2024. For predicting the stock price, the ARIMA-GARCH model has the lowest RSME. The findings suggest that volatility modeling is more accurate when combined with other methods in predicting a predictable stock market.
Introduction
The model developed by Shen, J., and Shafiq, M.O. outperforms traditional approaches to predicting stock trends due to feature engineering.
Yakup Kara, Melek Acar Boyacioglu, and Ömer Kaan Baykan developed ANNs and support vector machines to predict the Istanbul Stock Exchange National 100 Index. An ANN showed 75.74% accuracy versus 71.52% for an SVM.
Long Short-Term Memory (LSTM) networks were used by Adil Moghar and Mhamed Hamiche to predict financial time series.
The LSTM-ARO network proposed by Burak Gülmez outperforms other models. Lawi, A., Mesra, H., and Amir, S. optimized LSTM and GRU architectures for precise stock price predictions.
I created an LSTM model using news categories to predict Pakistan Stock Exchange (PSX) stock prices using Weighted and Categorized News (WCN-LSTM).
The Shanghai and Shenzhen markets were predicted by Qiao, R., Chen, W., and Qiao, Y. with refined LSTM models and rolling window analysis. With SMA, MACD, and RSI, Tran Phuoc and his colleagues predicted VN-Index and VN-30 stocks with 93% accuracy.
Time series data are usually analyzed using Autoregressive Integrated Moving Averages (ARIMAs). In one study, Aryio, A. O. Adewumi, and C. K. Ayo compared the predictions of ARIMA models.
Setyowibowo and colleagues demonstrated the effectiveness of ARIMA-GARCH models for predicting gold prices, as well as for predicting inflation.
In this study, I compare ARIMA, LSTM, MLP, and ARIMA-GARCH models for predicting NVIDIA stock prices over five years.
The Autoregressive Integrated Moving Average (ARIMA) model is an extension of the Autoregressive Moving Average (ARMA) model, which is widely used in statistics and econometrics for analyzing time series data. ARIMA enhances ARMA by handling non-stationary data, making it more adaptable. This model is particularly effective in managing data that exhibit trends or seasonal fluctuations by using a differencing process.
The ‘autoregressive’ (AR) component of the model deals with a variable that is regressed on its own previous values. If I denote
, where (Xt) is the observed value of the time series at time(t) and (Bi) is the lag operator that shifts the time series back by (i) time units, the AR operator of order (p) for an AR(p) process is given by the equation
Here, (ϕi) are the parameters of the autoregressive model, indicating the influence of the i-th lagged observation on the current value.
The ‘moving average’ (MA) component addresses the dependencies between an observation and the residual errors from a moving average model applied to lagged observations. The MA operator of order (q) for a MA(q) process is represented by the equation
In this equation, (θi) are the parameters of the moving average model, representing the impact of the i-th lagged forecast error on the current value.
The ‘integrated’ (I) part of ARIMA involves differencing the original observations, which is a crucial step in converting non-stationary data into stationary data that is suitable for further analysis. The differencing operator, denoted as
represents the d-th difference of the time series (Xt).
Combining these components, the ARIMA model can be expressed as
In this equation,
where (μ) is the mean of the series after removing any existing trend from the differencing step,(εt) is the error term (or white noise) at time (t), which is the unpredictable random error.
An MLP is a type of neural network used in machine learning. It mimics how the human brain processes information. It has several layers: input, hidden, and output. Each layer is fully connected through weights and biases.
MLPs model complex relationships in data by calculating weighted sums and applying nonlinear functions. They improve using backpropagation and loss minimization during training.
Data models can be created using MLPs to predict and work with new data.
LSTMs are advanced Recurrent Neural Networks (RNNs). They are designed to handle long sequences of data that traditional RNNs cannot handle, like vanishing and exploding gradients. It is important to understand patterns over time by using RNNs to influence current outputs based on previous inputs.
There are three gates in LSTMs: the forget gate, the input gate, and the output gate. These gates control what information is retained, added, or passed.
A forget gate makes a decision about what should be kept or deleted from a cell's memory by taking into account the old hidden state and the current input. Mathematically, it is:- The input gate and candidate cell state decide what new information should be added. The input gate is calculated similarly to the forget gate:
And the candidate cell state is: