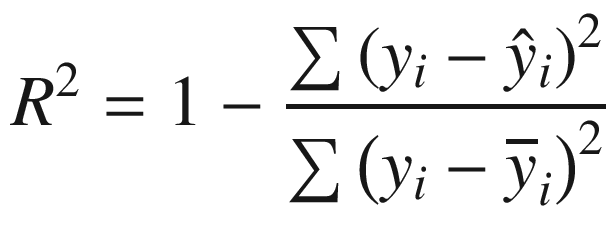ML Model Evaluation For Forecasting
The build phase of a machine learning model typically involves benchmarking multiple models.
Afterward, you estimate the performance of those models and choose the one you think is most likely to succeed. In order to determine which forecast to keep as your actual forecast, you must use objective measures of performance.
You will discover a variety of tools for evaluating models in this chapter. You will learn how to evaluate machine learning models in general and specific considerations and adaptations for forecasting. In addition, different metrics will be used to score the performance of the models.
A forecast example for evaluation
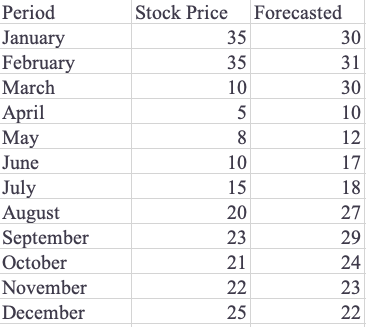
In Table 1, we look at a hypothetical example of stock prices per month in 2020 and the forecast made by someone for this. In this case, assume that the forecast was created in December 2019 and has not been updated since then.
As you can see, there is a considerable difference between the actual and forecasted values. However, things like that do happen. Using snippet 1, let’s plot the two lines using the data in Python.
This should give you the graph in Figure 1, which shows the forecasted values against the actual values.
Using Table 2, we can now calculate the differences between forecasted values and actual values.
Metrics for Model Quality
In order to improve the model, it is useful to know the month-by-month error. Although it gives a first impression of the model’s quality, this method of evaluating models has some limitations. The first problem is that this level of detail isn’t appropriate for a model comparison; you can’t compare long lists of errors between models, but you ideally want one or two KPIs.
Furthermore, you should note that this Error column cannot simply be taken as an error metric and averaged. The positive and negative error measures will average out since they are both positive. Your error would be underestimated by this amount.
By taking the absolute values of the errors or by squaring them, you can solve this problem. In this way, you will ensure that a negative error does not cancel out a positive error. Five common metrics are now available for you to choose from.
Metric 1: MSE
One of the most widely used metrics in machine learning is the Mean Square Error (MSE). The average of squared errors is calculated. MSE is calculated by taking the average of the errors per row of data, squaring those errors, and then taking the average of those squares.
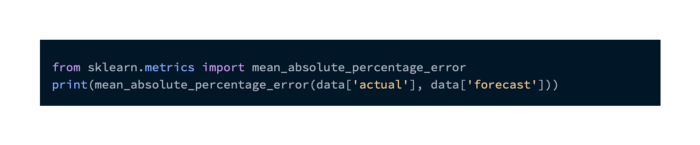
Python’s scikit-learn library can be used to compute it, as shown in snippet 2.
This gives a MSE of 53.7 in the current example.
Error metrics are based on a multifaceted logic. In the first place, it is clear why the squared errors are used rather than the original errors, since summating the original errors is impossible. As the original errors contain positive and negative values, they would cancel each other out. The sum of two large errors may be close to zero if there is a large negative error and a large positive error, which is clearly incorrect. In order to counter this, you can use the square root of the value, which is always positive.
Additionally, it functions as an average, which is another part of the formula that you can understand. Dividing the sum of all values by the number of observations gives you the number of observations. A MSE is calculated by averaging the squared errors.
Comparing different models on the same dataset is easy with the MSE error metric. For each model applied to the same dataset, the MSE will be the same. It is difficult to interpret the metric outside of benchmarking multiple models because the scale is not intuitive.
A smaller error indicates a better model, so the MSE is an error metric. Because the metric lacks a fixed scale, it cannot be converted into an accuracy measure. The error has no upper bound, so it should be used only for comparison.
Metric 2: RMSE
In mathematics, the Root Mean Squared Error (RMSE) is defined as the square root of the Mean Squared Error. Using the MSE square root for classifying performances in order does not make any difference when you want the error metrics.
In spite of this, using RMSE over MSE has an advantage. Because the RMSE has the same scale as the original variable, we take the square root of the MSE. MSE is calculated by taking the average of squared errors. This makes it difficult to interpret the value. Your actual values will be scaled back to the error metric by using the square root.
With snippets 3, you can calculate the RMSE and find that it is 7.3. Your actual stock prices are much closer to this. For explanations and communication, this can be helpful.
A lower RMSE indicates a better model, since it is an error measure.
Despite its intuitive appeal, RMSE still depends on actual values to determine its scale. In the same way that MSE cannot be compared between datasets, RMSE cannot.
Metric 3: MAE
By taking the absolute differences between predicted and actual values per row, Mean Absolute Error (MAE) is defined.
An absolute error’s mean is its average.
It is important to note that the MAE takes the absolute value of the errors before averaging them. By taking the average of absolute errors, we can prevent errors from canceling each other out when summing them.
A MAE is another method of avoiding this, as you have seen with the MSE. In most cases, people intuitively come up with the MAE as the error metric. Even so, RMSE tends to be preferred over MAE in most cases.
In mathematical computations that require derivatives, the RMSE is more straightforward to use since it uses squares rather than absolute values. There is a great deal more ease in computing the derivative of squared errors than the derivative of absolute errors. Due to the importance of the derivative in optimization and minimization, this criterion is important.
RMSE and MAE can be interpreted similarly. Neither produces scores that are out of range with the actual values. It is inevitable that the MAE and MSE will differ. The squared errors may be weighted more heavily in the total evaluation if one of the individual errors is very high. In spite of this, it is not possible to determine whether one measure of error is better or worse than another.
Using the code in snippet 4, you can calculate the Mean Absolute Error in Python. The MAE should be 5.67.
Metric 4: MAPE
A MAPE is calculated by dividing the actual value by the error for each prediction. Using this method, errors are calculated relative to actual values. As a result, the error will be measured as a percentage, and therefore it will be standardized.
In the previous error measures, you saw that they weren’t standardized. However, this standardization is extremely useful. Communication of performance results is made very easy by this method.
MAPE is computed by taking the absolute values of those percentages per row and averaging them. You will obtain 0.46 from snippet 5.
Percentages of error are measured by the MAPE. A lower MAPE value indicates a better measurement of error. A goodness of fit measure can be calculated by computing 1 — MAPE. Performance is often better communicated in terms of positive results rather than negative results.
Even though the MAPE function is intuitive, it has one critical drawback: it divides the error by the actual value when the actual value is 0. Mathematically, this results in a division by zero. It is therefore difficult to use.
Metric 5: R2
In terms of metric, the R2 (R squared) metric can be compared to 1 — MAPE very closely. The metric is performance-based rather than error-based, so communication is greatly enhanced.
An R2 value is typically between 0 and 1, with 0 being a bad value and 1 being a perfect value. Thus, multiplying it by 100 makes it easy to use as a percentage. Only a forecast that is more than 100% off can result in a negative R2.
There is an interesting computation done by the formula. In this formula, the sum of squared errors is divided by the sum of deviations between forecast and average. As a result, your model will be more accurate than using the average as a model. Your model will have a R2 of zero if it makes the same prediction as the average. The average is a very practical performance metric since it is often used as a benchmark.
Using Python, you can calculate R2 using the code listed in snippet 6.
You get a value of 0.4 (rounded). Based on an R squared scale of 0 to 1, this could be translated as 40% better performance than the average. Using percentages to track model performance is very effective in many situations, although this exact interpretation may not be obvious to your business partners and managers.
Strategies for evaluating models
Let’s now look at how to set up tests for model comparison now that you’ve seen five key metrics. It is common to work with multiple models at once when doing advanced forecasting.
In general, you need to decide which model is the most accurate once you’ve worked with all those different models.
A number of models could be used to predict the (short) future and then tested to see which one worked best. In practice, this happens, and it’s a good way to deliver quality forecasts. It is possible to do more, however. In order to estimate errors, it would be more interesting to use past data rather than wait.
In practice, how can we determine which model is most accurate without having to wait until the future?
Out-of-Sample Error and Overfitting
The purpose of forecasting is to build models based on historical data and then project them into the future. There are certain biases to avoid when doing this. It is common to fit a model on historical data, compute errors, and use the errors for forecasting if the errors are good.
However, due to overfitting, this won’t work. When a model is overfit, it learns the past data too precisely. With the advanced methods available on the market, models are capable of fitting almost any historical trend to 100%. Out-of-sample prediction performance is not guaranteed by this formula.
The performance of overfit models is poor when compared with historical data. An overfitted model projects past noise into the future instead of learning general, true trends.
The power of machine learning is that it can learn anything you give it. Overfitting, however, leads to too much learning. There are several strategies that can be used to prevent this from happening.
Train-test split is the first strategy
One of the most common splits is the train-test split. Data is split into two rows when you apply a train-test split. The data in a test set should usually be kept at 20% or 30%.
The rest of the data: the training data, can then be used to fit models. There are many models that can be applied to train data and predicted based on test data. The models with good performance on the train data do not necessarily perform well on the test data when you compare their performance on the test set.
In a model with an overfit, the training data score is higher than the test data score. Typically, a model with a lower error on training data will outperform a model with a higher error on test data.
In order for the test performance to be representative of the future forecast, it should be based on data that is “unknown” to the model, which simulates the future forecast situation.
Choosing a test set is the next question that you could ask. Typically, machine learning problems are solved by randomly selecting data for the test set. However, forecasting in this case is quite specific. The test set should be the last 20% observations since you usually have an order in data: this will simulate the future application of forecasting.
Let’s take a look at a very simple forecasting model to illustrate the train-test split: the mean model. This method involves taking the average of the train data and using that as a forecast. Even though it is not very performant, forecasting models often use it as a “minimum” benchmark. Models worse than this should not even be considered.
Let’s use the stock price data from before using snippet 7 as an example.
As a result, the train error will be 122.9375 and the test error will be 32.4375. It is important to note that with one year’s worth of data, a train-test split will cause problems. There will not be a full year of training data, so the model will not be able to learn any seasonality. The training data should also have three observations per period (in this case, three years).
Selecting the testing period should take seasonality into account. Often, test sets of 20% and 30% of the data are used in non-forecasting situations. My recommendation for forecasting is to use a full seasonal period. Using a full year as a test period is recommended if you have yearly seasonality, to avoid having a model work well in summer but not well in winter (possibly due to different dynamics in seasonal forecasting).
Strategy 2: Train-Validation-Test Split
When you compare models, you benchmark their performances. In order to avoid overfitting, you can train the models on the train set and test them on the test set.
An additional split can be added to this approach: the validation split. By using the train-validation-test split, you train models on the training data, benchmark them on the validation data, and then select the best model based on the benchmarking data. Using your selected model, you then compute an error on the test set: this should confirm your model’s estimation.
The validation error is underestimated if the error on the test sets is significantly worse than the error on the validation sets. This will alert you that the model isn’t as good as you expected.
It is important to note that a lot of data is dedicated to model comparison and testing when using the train-validation-test split. In light of this, it is recommended to avoid using this approach when working with limited data.
Validation and test data should be left out of the validation and test periods, as discussed previously. You will miss two of the most recent years of data if, for instance, you decide to use three years of monthly data for training, one year for validation, and one year for testing.
The optimal model could be selected (i.e. model type and optimal hyperparameters); and the optimal model could then be retrained using the most recent data once it is selected and benchmarked.
The snippets 8 show two models being compared: the mean and the median. Model comparison should not be based on performance: we are only demonstrating how to use validation data for model comparison.
According to the example, the mean model has a validation MSE of 23.56 and the median model has a validation MSE of 91.25. This would suggest that the median model should be retained rather than the mean model. A final evaluation is to determine if the validation error is not influenced by a set of validations that is (randomly) favorable to the mean model.
By taking a final error measure on the test set, this can be accomplished. Due to the fact that both the validation and the test sets were unseen data, their errors should be close. However, you find that the test MSE is 41.3125, almost twice as large as the validation MSE. You may have a bias in your error estimation if the test error differs greatly from the validation error. The bias here is rather obvious: the validation set has too few data points (only two data points), resulting in a false error estimate.
You would have been able to get an early indication of the error metrics of your model from the train-validation-test set. Therefore, you could not rely on this forecast in the future. Evaluation strategies cannot improve models, but they can certainly improve your choice of forecasting models! Your model’s accuracy is therefore indirectly affected by it.
Strategy 3: Cross-Validation for Forecasting
Having very little data can cause problems with the train-test set. It is not always possible to keep 20% of the data separate from the model. Cross-validation is an excellent solution in this case.
Cross-validation using K-Fold
There are several types of cross-validation, but K-fold cross-validation is most common. Cross-validation K is like adding to train-test split. Each model’s error is calculated only once, on the test data, in the train-test split. The K-fold cross-validation method involves fitting the same model k times and evaluating each error. The average is then calculated based on k error measures. This is the error you got from your cross-validation.
This can be accomplished by dividing the train-test data into a number of different splits, such as a K-fold cross-validation. In the case of k = 10, the data will be divided into ten parts. Each of the ten parts will then be tested once. As a result, nine of the remaining parts are used for training purposes.
For k, you are generally looking at values between 3 and 10. When you go much higher, you will have smaller test data, which can lead to inaccurate error estimates. You lose the cross-validation value if you go too low and have very few folds. The train-test split is simply applied when k = 1.
As an example, imagine a 100-point case with a fivefold crossvalidation. Based on the schematic illustration in Figure 2, you will create five different train-test datasets.
Training the model on the training data enables you to compute the error on the test data, and testing the model on the test data allows you to train the model again. When the five test errors are averaged (snippet 9), the cross-validation error can be calculated.
You will get a cross-validation error of 106.1 in this example. A MSE shouldn’t be compared to errors of other models on the same dataset since it is a MSE.